一、别名
二叉搜索树, 有序二叉树, 排序二叉树, Binary Search Tree
二、特征
- 左子树的所有节点的值均小于根节点
- 右子树下所有节点的值均大于更节点
- 所有节点的值都不相同
- 任意节点的左子树和右子树也都是BST

三、节点结构
1
2
3
4
5
6
7
8
public static class Node {
// 数据区
private int data;
// 左节点
private Node left;
// 右节点
private Node right;
}
四、实现概述
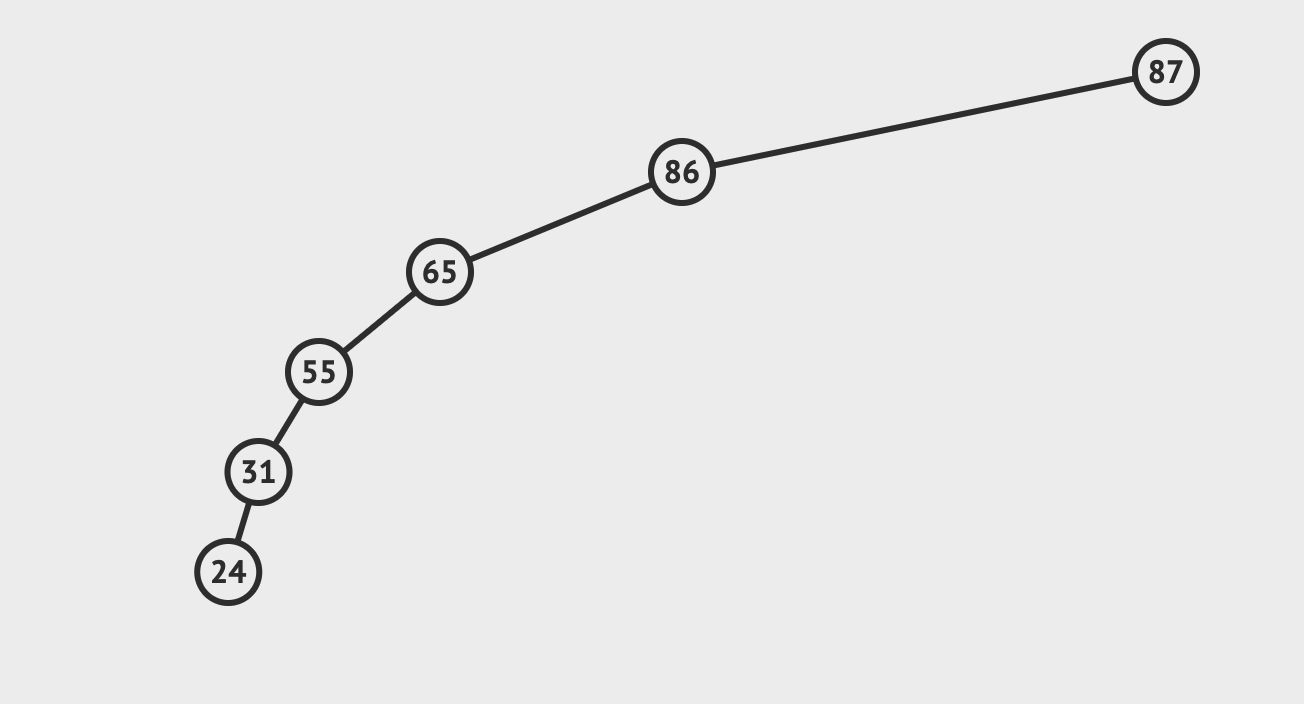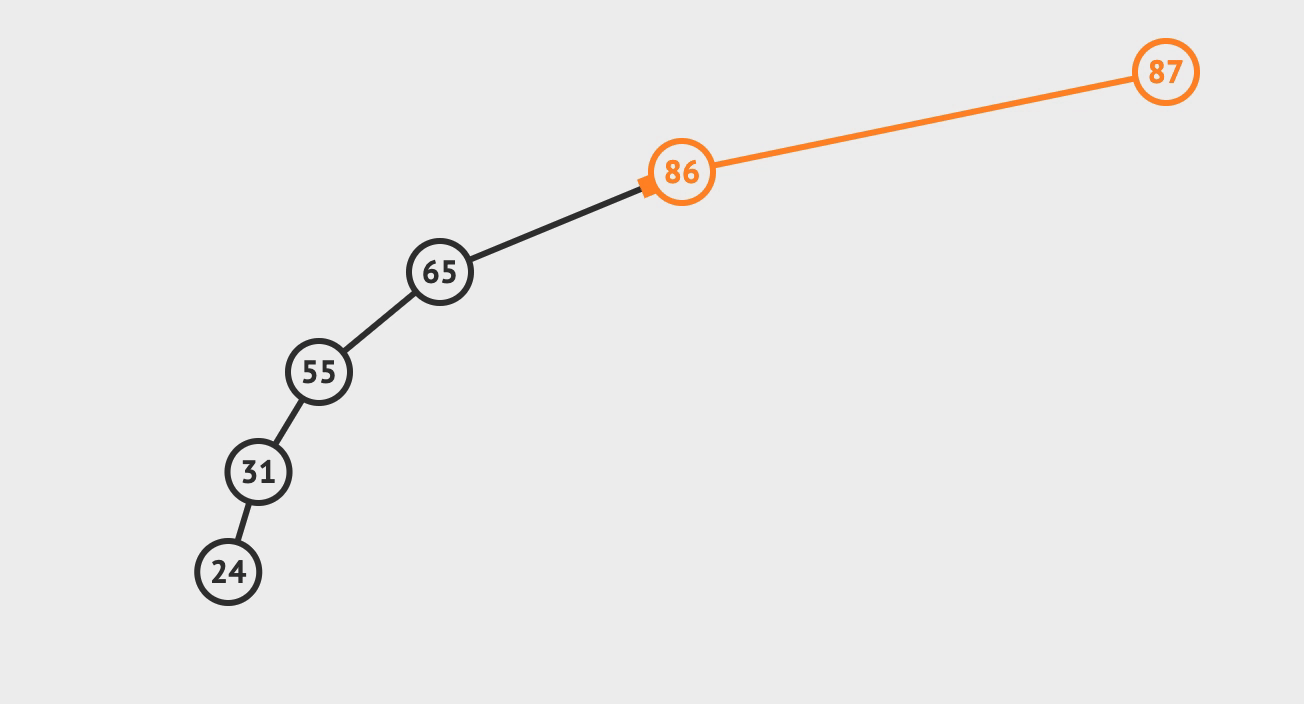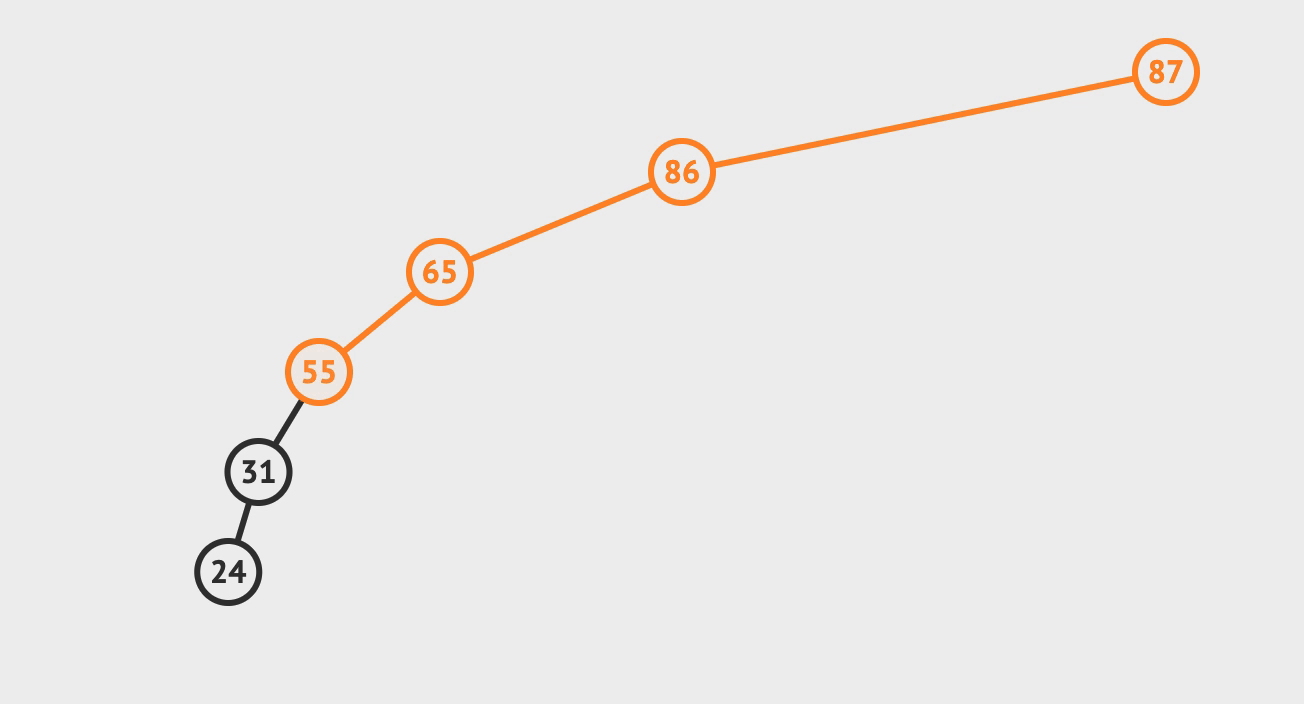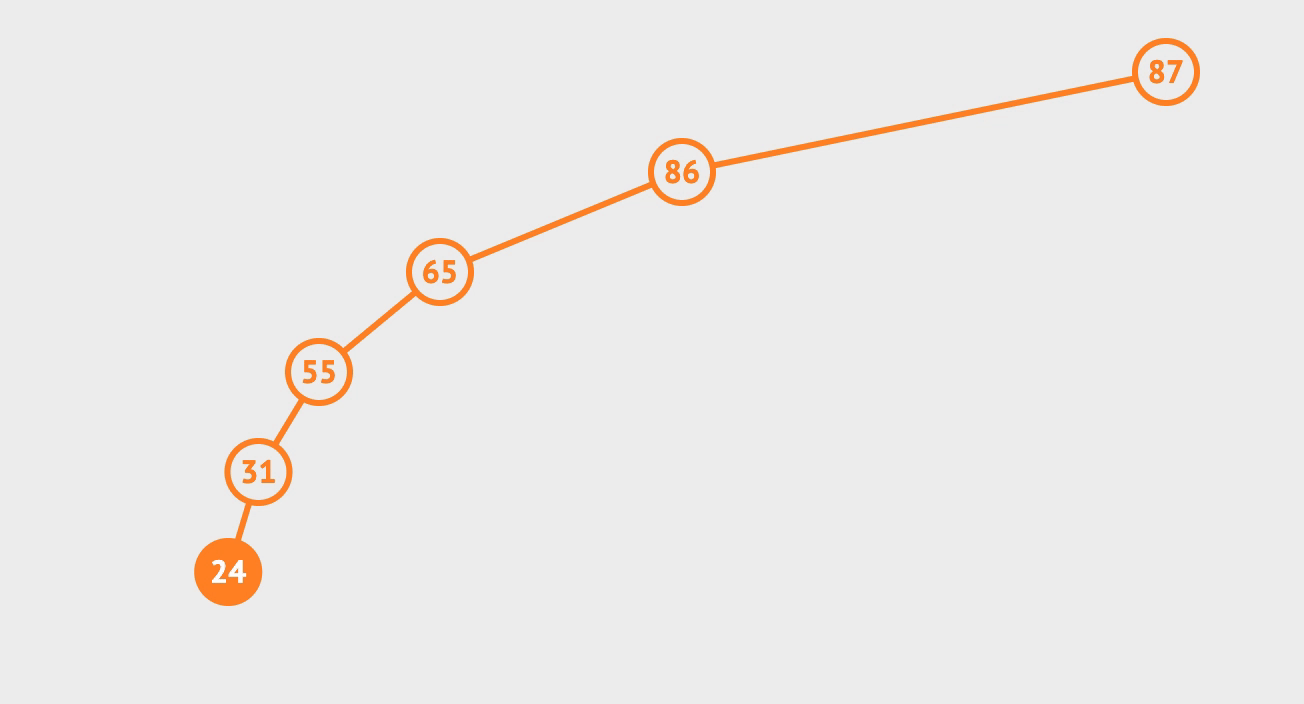
1. 查找
- 先查找根节点,
< 根, 则找左子树;> 根, 则找右子树;= 根, 则找到返回;
算法时间复杂度 对于 n 个节点的树
最优f(n) = 需要查找的次数 = 二叉树的层数 ~= O(logn)
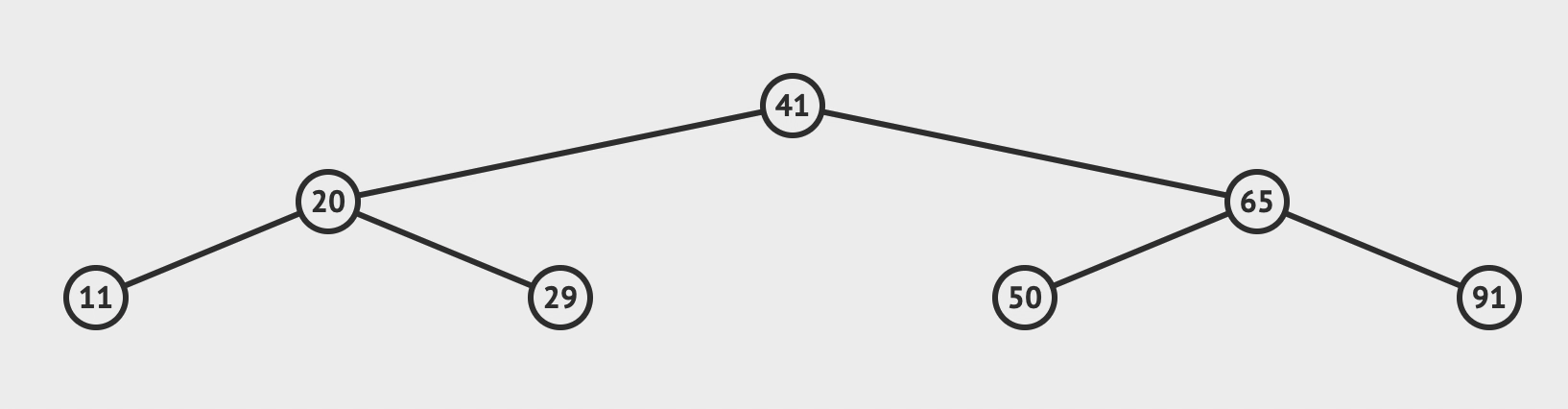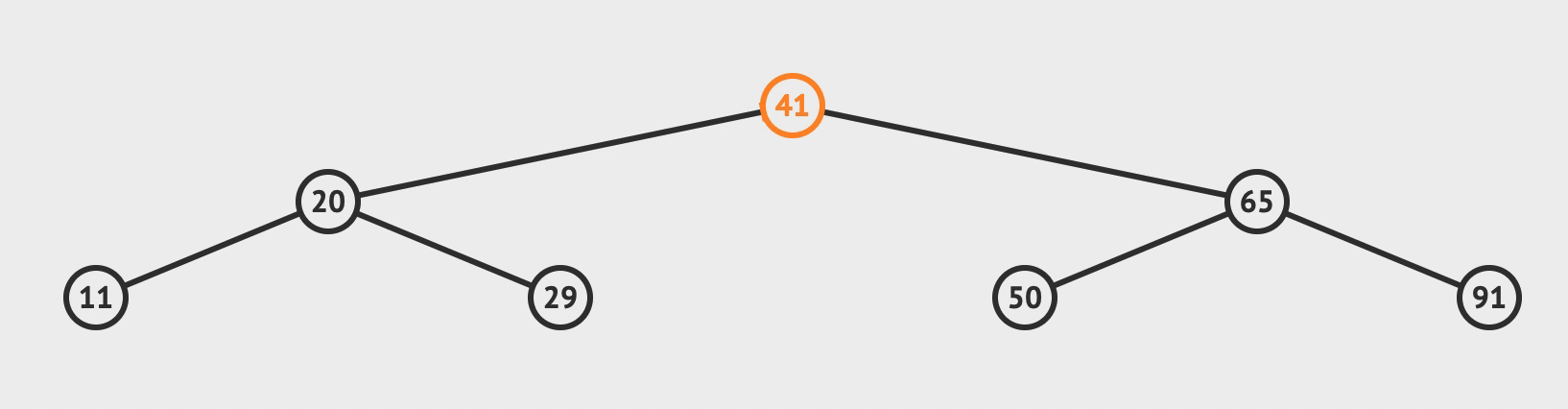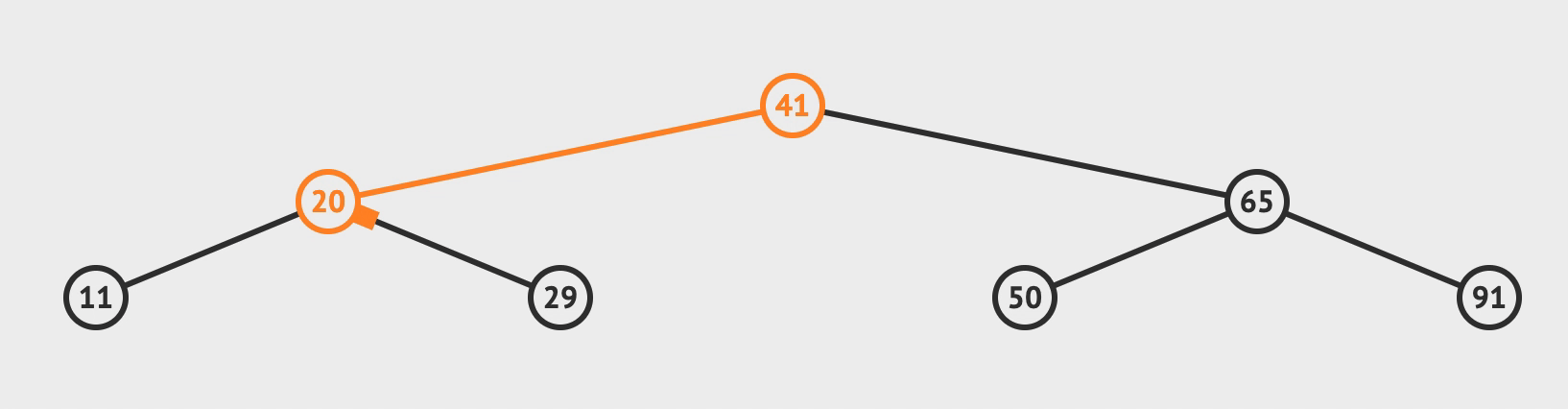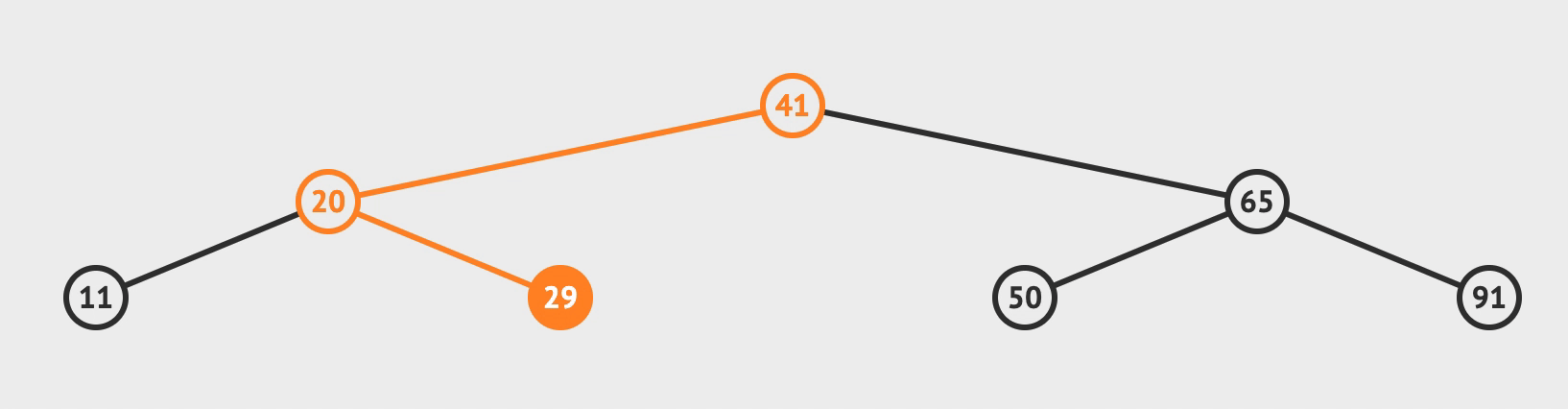
最差f(n) = 需要查找的次数 = 二叉树的层数 = n = O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public Node search(int num) {
return doSearch(root, num);
}
private Node doSearch(Node root, int num) {
if (root == null) {
return null;
}
if (root.data == num) {
return root;
} else if (root.data > num) {
return doSearch(root.left, num);
} else if (root.data < num) {
return doSearch(root.right, num);
}
return null;
}
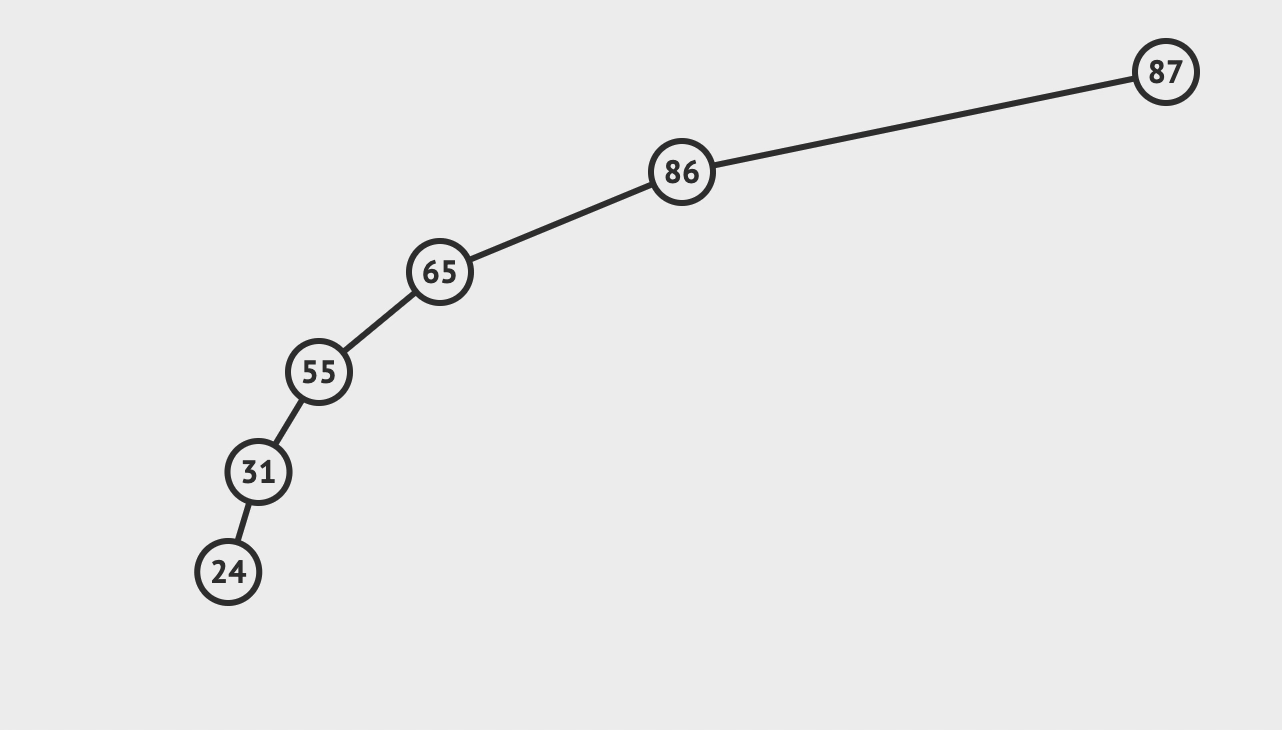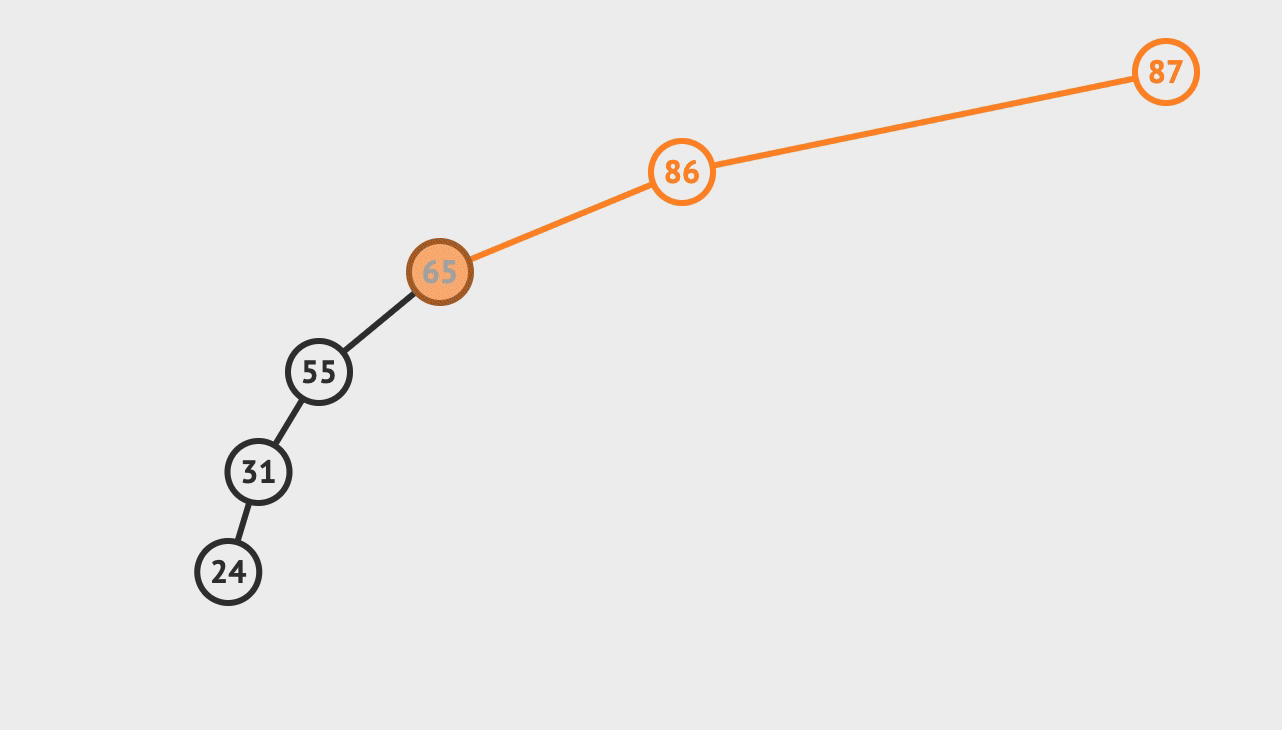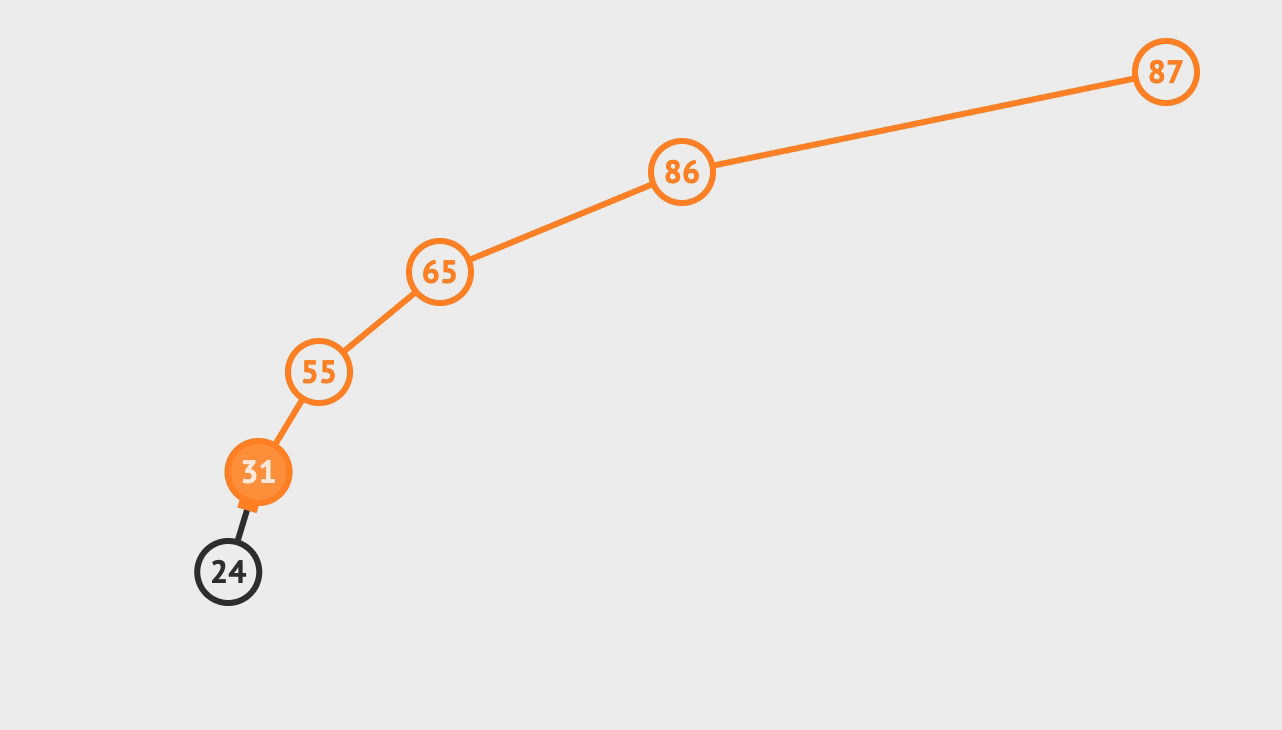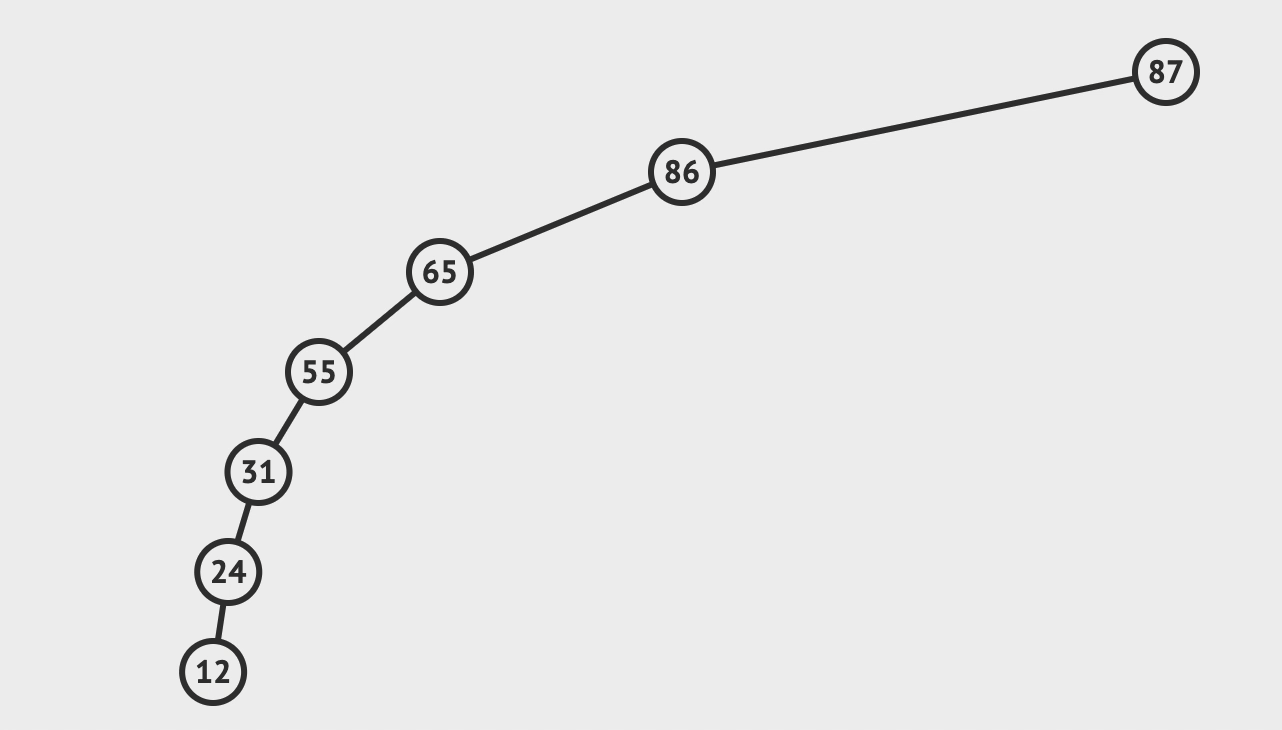
2. 插入
- 比对根节点, 小于就往左节点比对, 大于就往右节点比对
- 直到需要比对的节点为空, 而这个空就是你需要插入的位置
算法时间复杂度:
-
最优f(n) = 需要比对的次数 = 二叉树的层数 ~= O(logn)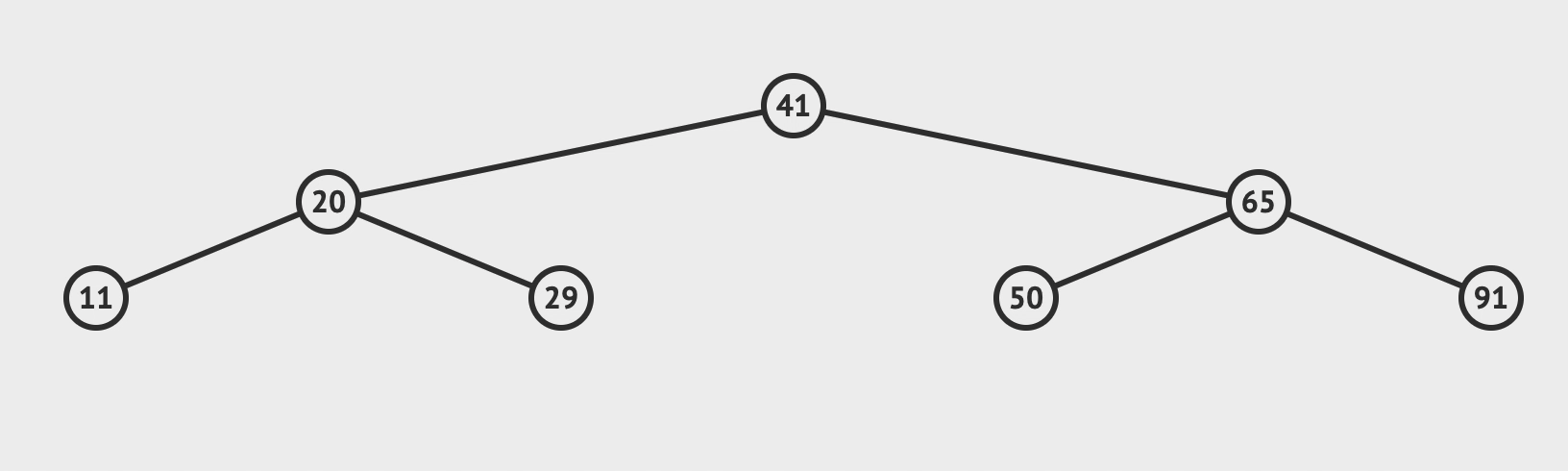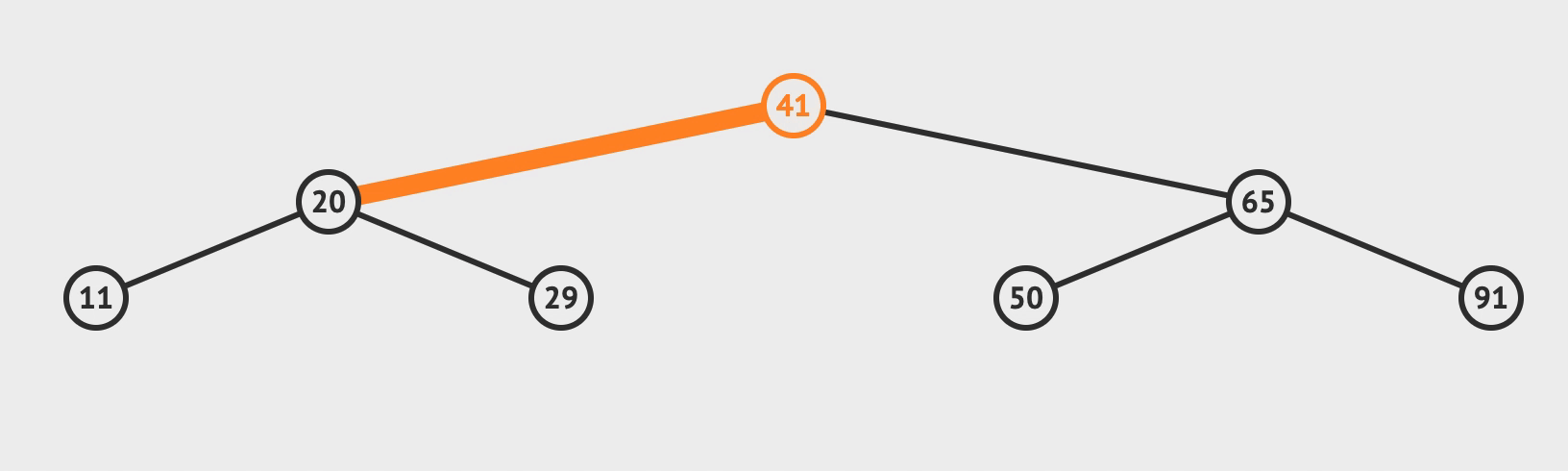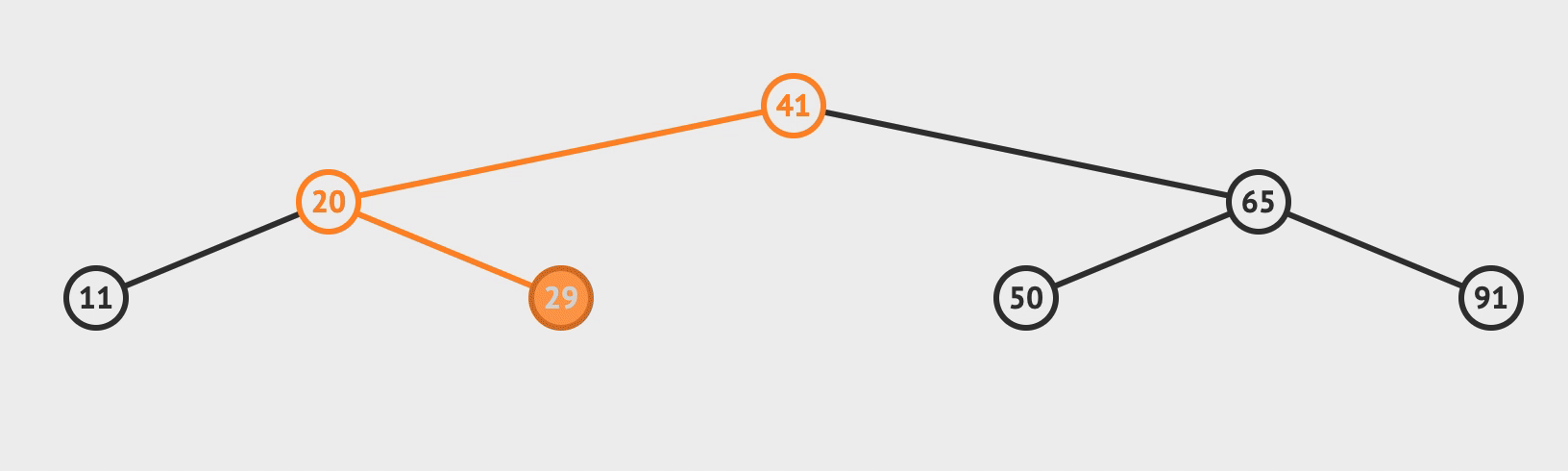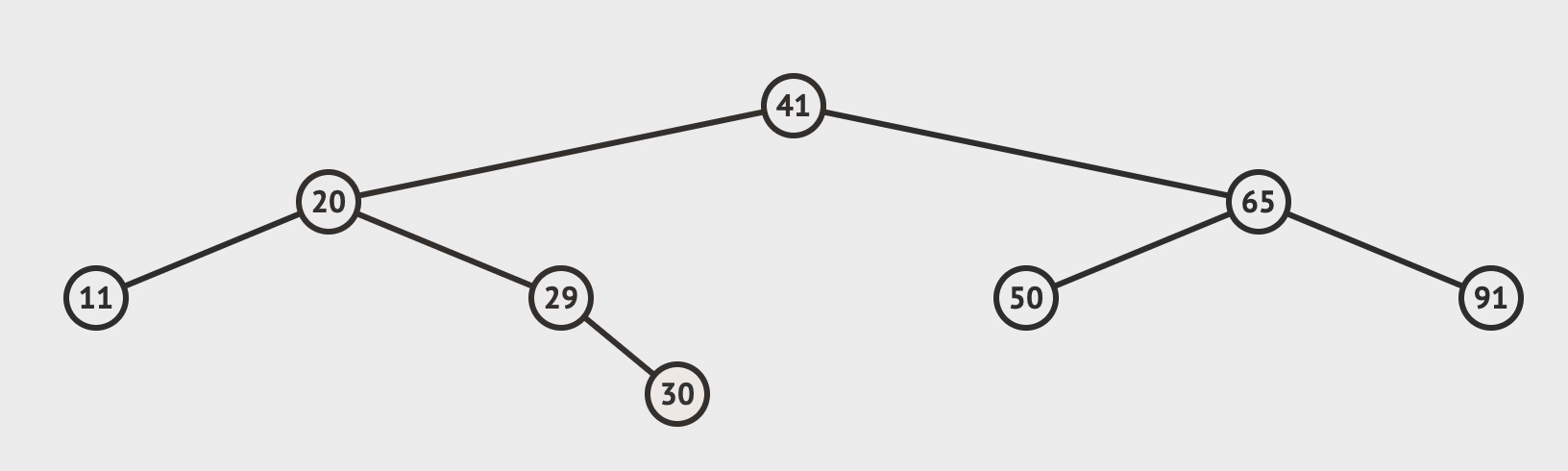
-
最差f(n) = 需要查找的次数 = 二叉树的层数 = n = O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public void insert(int num) {
root = doInsert(root, num);
}
private Node doInsert(Node parent, int num) {
if (parent == null) {
parent = new Node(num);
} else if (num > parent.data) {
parent.right = doInsert(parent.right, num);
} else if (num < parent.data) {
parent.left = doInsert(parent.left, num);
}
return parent;
}
3. 删除
- 先查找到目标节点
- 若: 目标左子树为空, 则, 用目标右子树根节点替换目标
- 若: 目标右子树为空, 则, 用目标左子树根节点替换目标
- 若: 都不为空, 则, 选取
左子树值最大节点或者右子树最小节点替换目标, 并, 递归删除替换目标的节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
public void remove(int num) {
root = doRemove(root, num);
}
private Node doRemove(Node parent, int num) {
if (parent == null) {
return null;
}
if (num > parent.data) {
parent.right = doRemove(parent.right, num);
} else if (num < parent.data) {
parent.left = doRemove(parent.left, num);
}
// 找出左子树最大的值或者右子树最小的值替换, 这里选择前者来实现
else if (parent.left != null && parent.right != null) {
// 找到左子树最大值替换
parent.data = findMax(parent.left).data;
// 删除左子树中用于替换的节点
parent.left = doRemove(parent.left, parent.data);
}
// 左子树为空, 直接用右子树根节点替换被删除的节点
else if (parent.left == null) {
parent = parent.right;
}
// 右子树为空, 直接用左子树根节点替换被删除的节点
else if (parent.right == null) {
parent = parent.left;
}
return parent;
}
private Node findMax(Node node) {
if (node == null) {
return node;
}
while (node.right != null) {
node = node.right;
}
return node;
}
算法复杂度:
-
最优f(n) = 需要比对的次数 = 查找到目标比对次数 + 递归查找替换目标的节点的替换节点的比对次数 = 二叉树层数 = O(logn)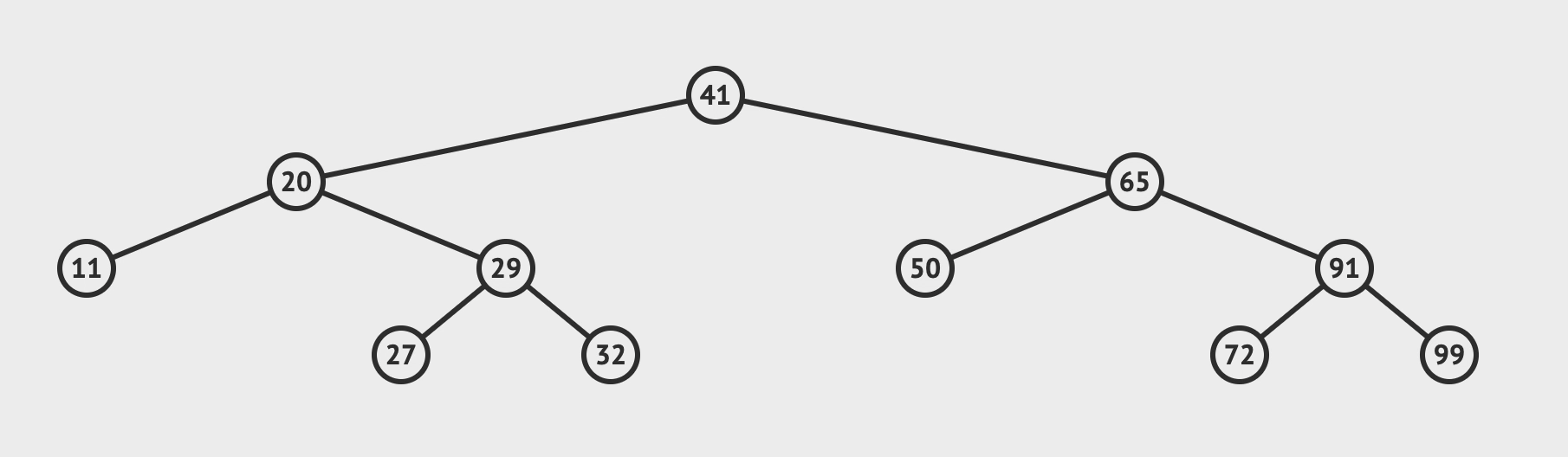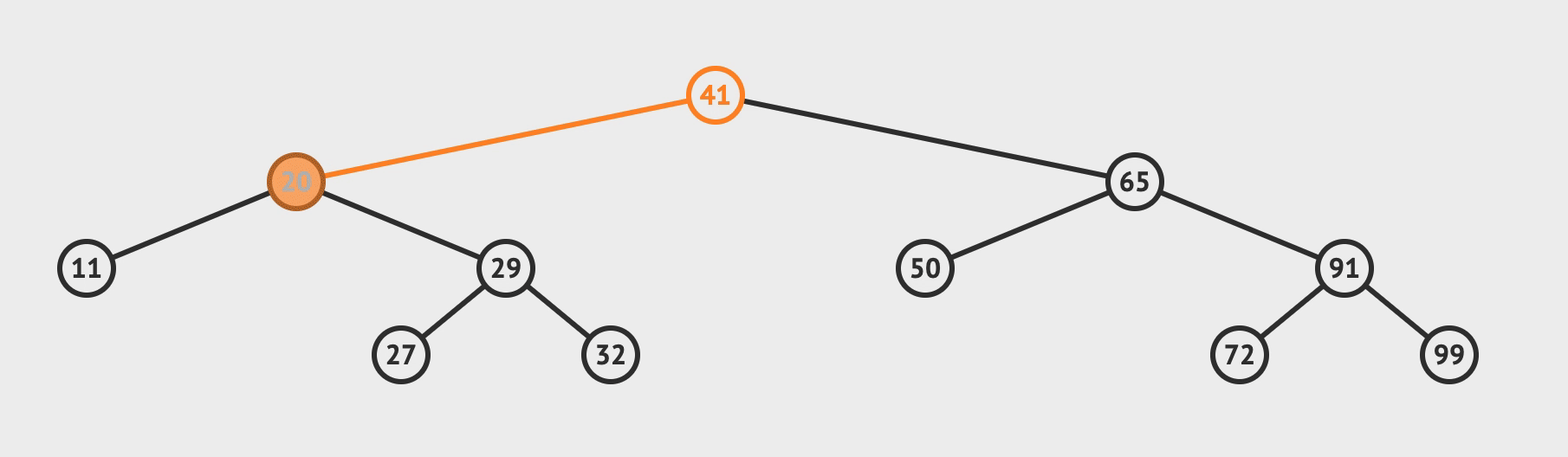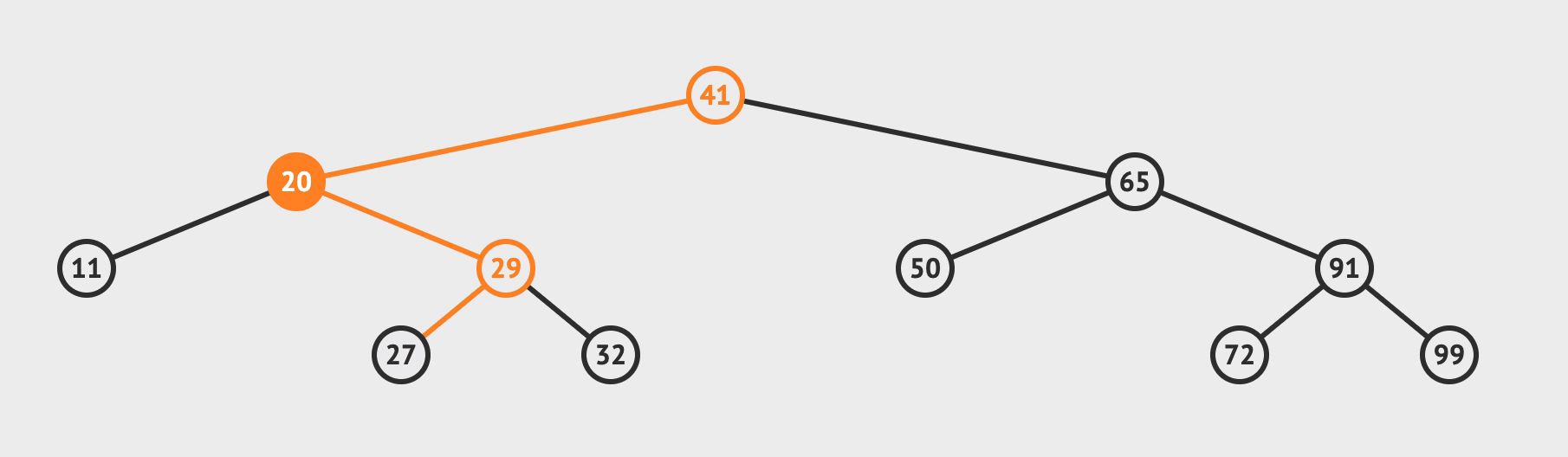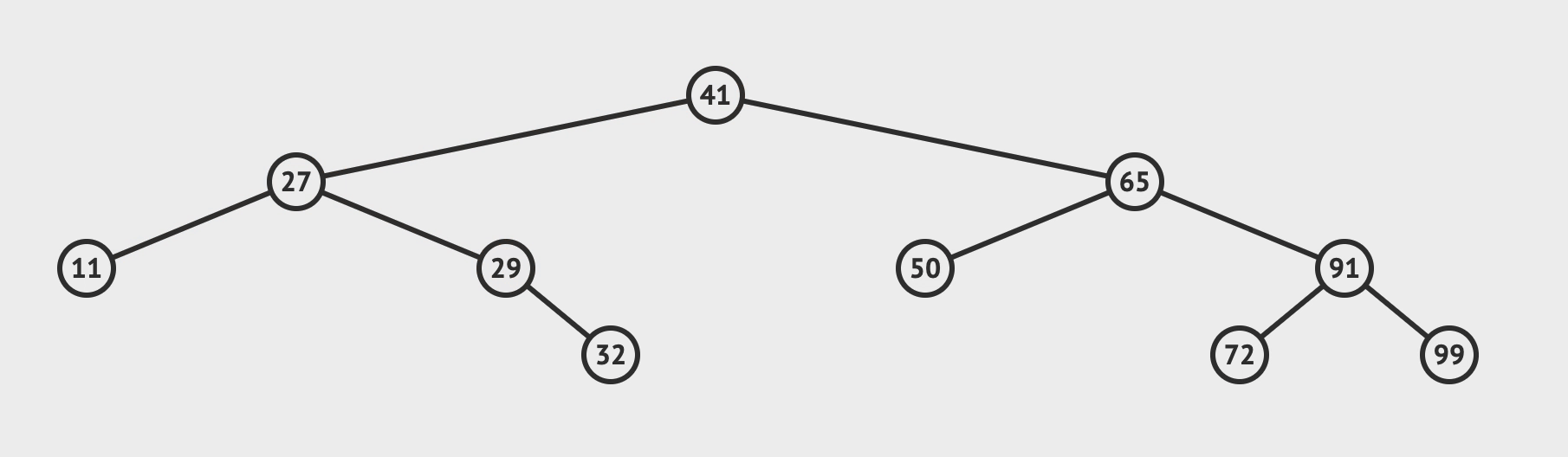
-
最差f(n) = … = 二叉树层数 = n = O(n)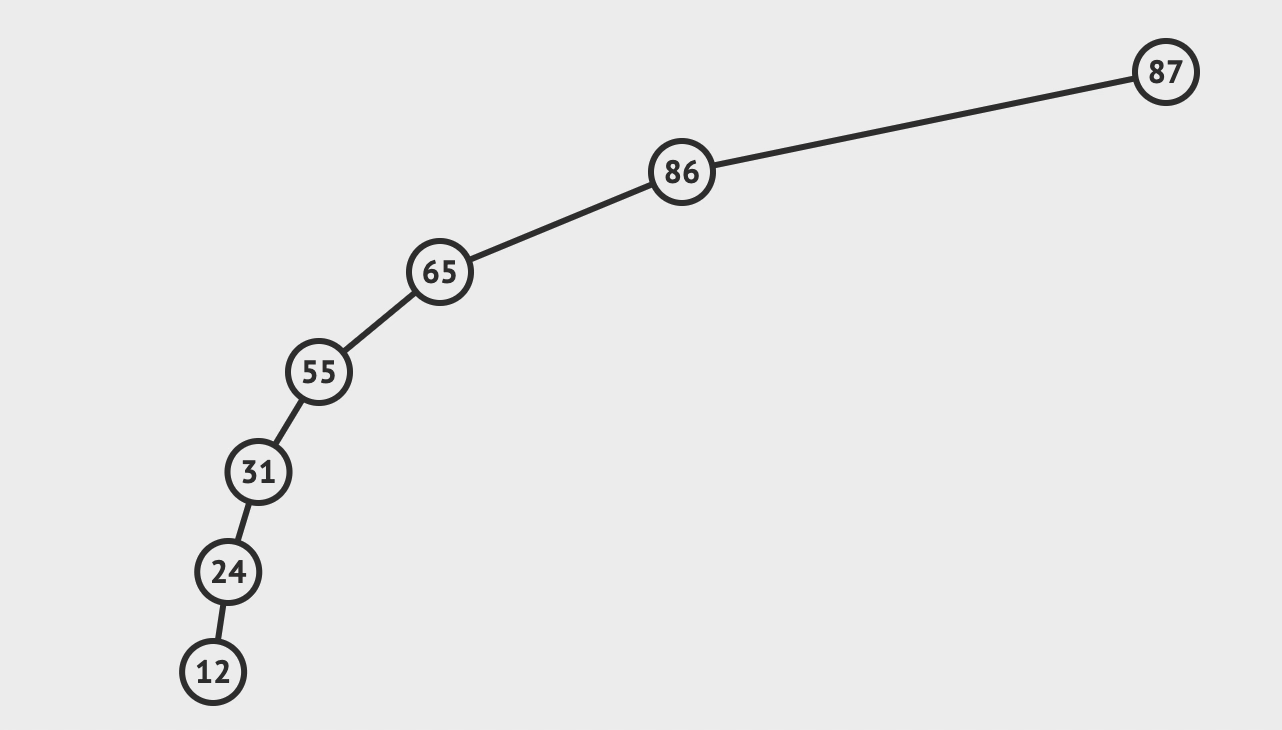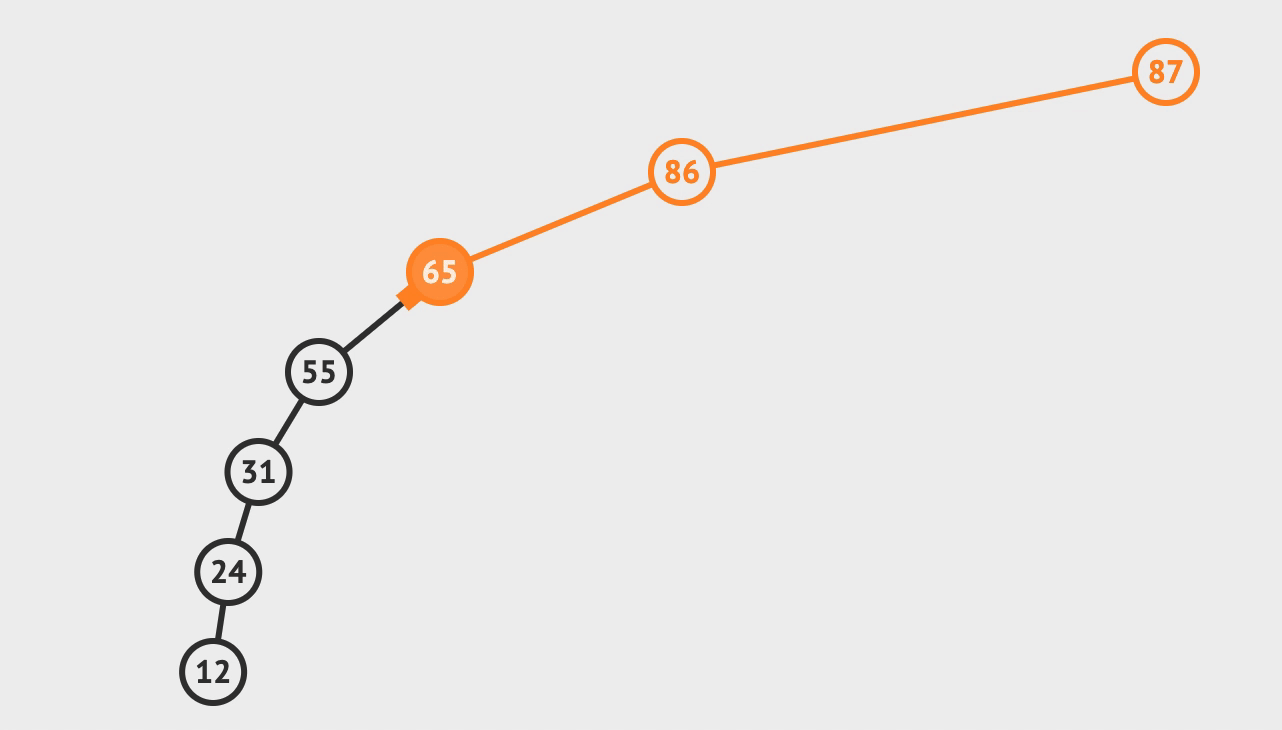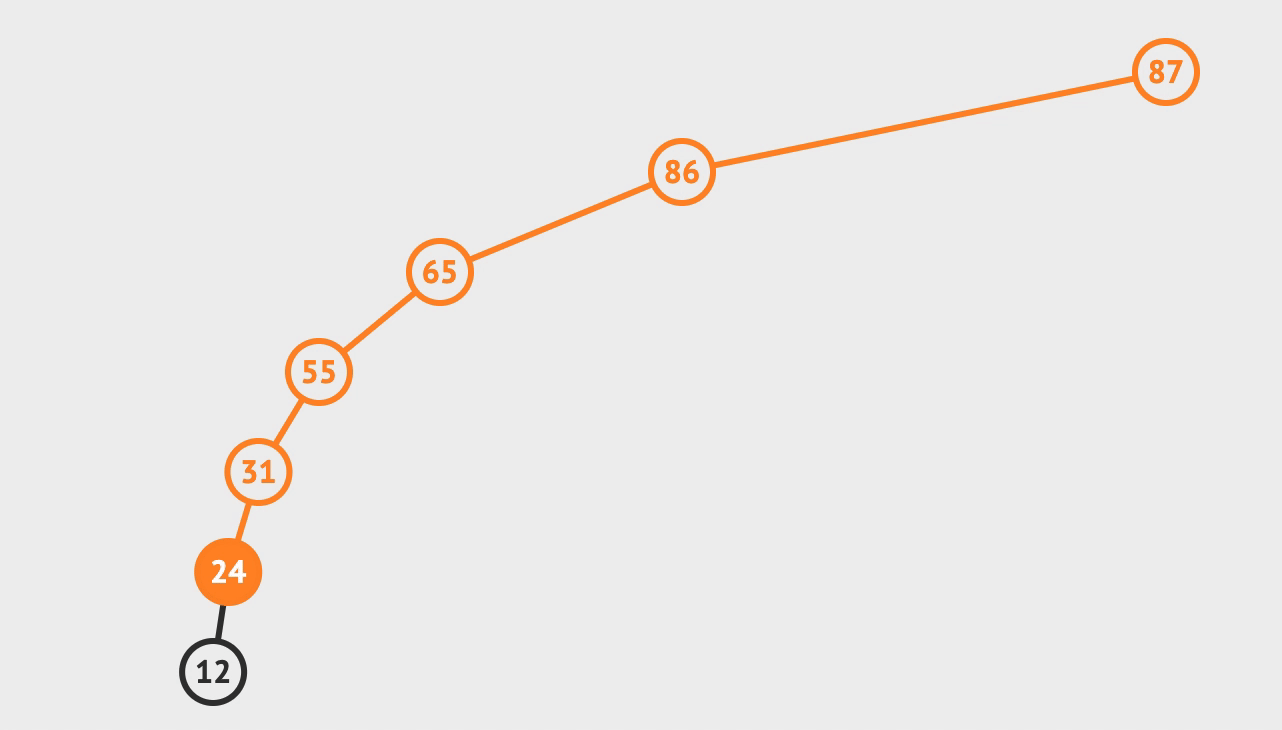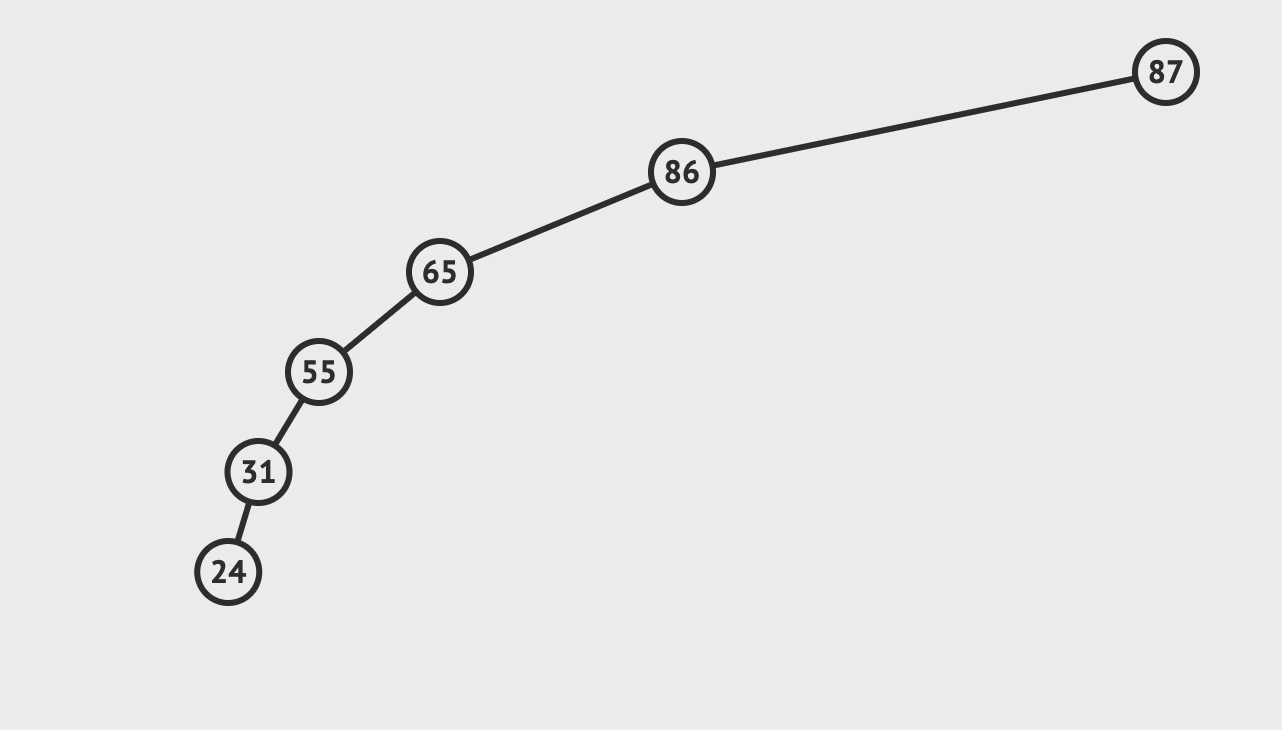
具体实现
就一个BinarySearchTree.java文件搞定, 里面还附有main()函数测试功能, 可直接运行github传送门