一、须知须会
-
平衡因子: 二叉树的 左子树 - 右子树 = 高度的差值,在平衡树中可能的值(-1 ,0 ,1) -
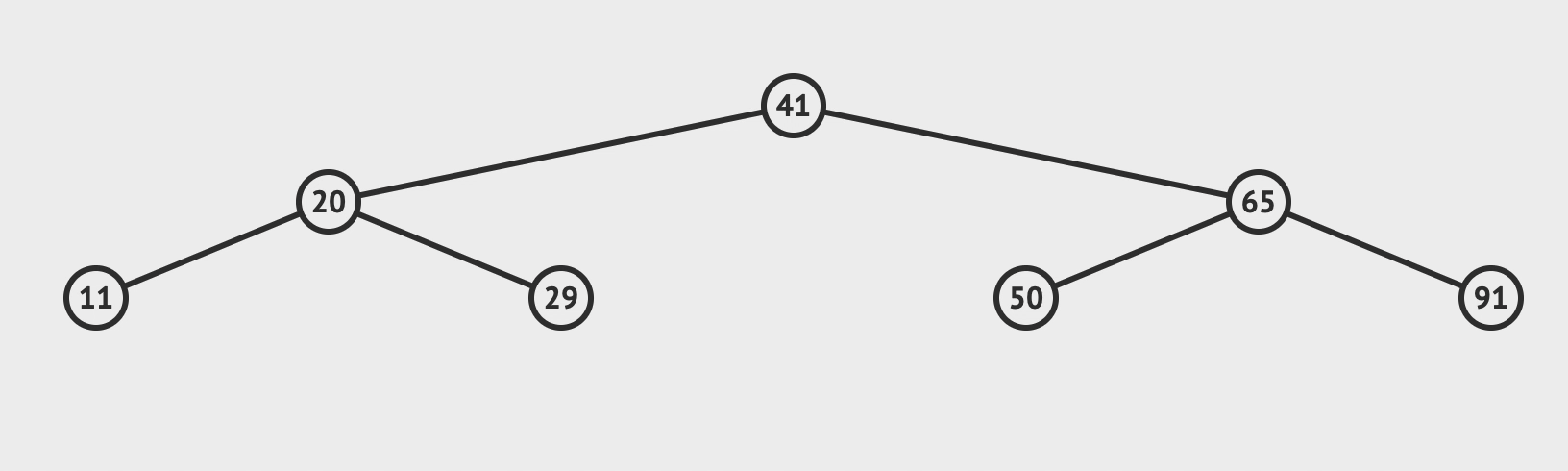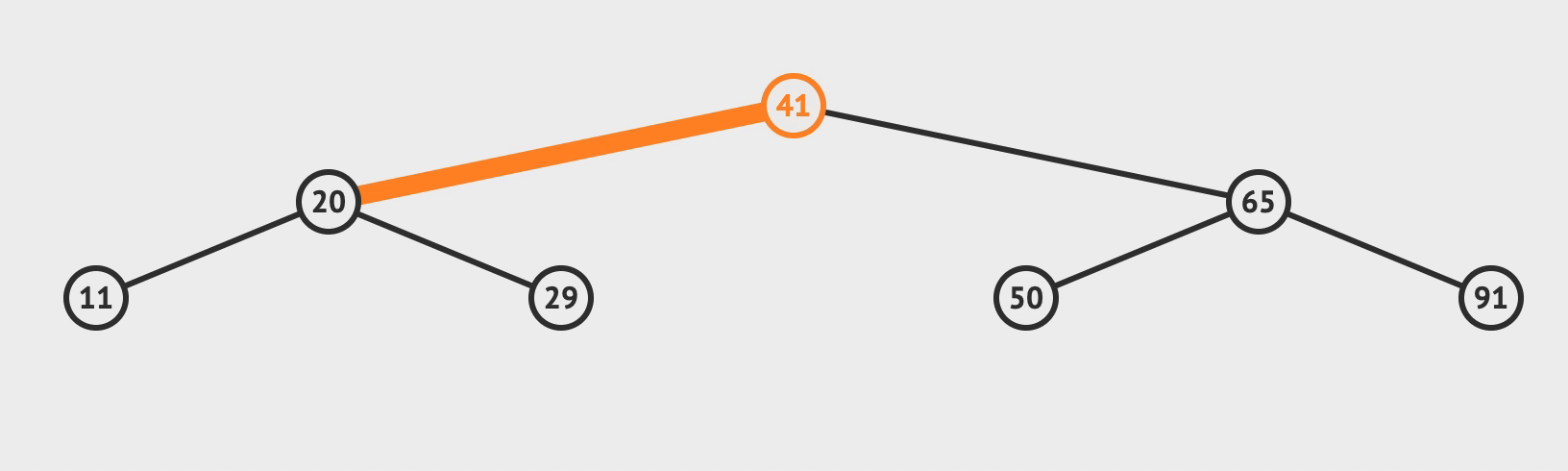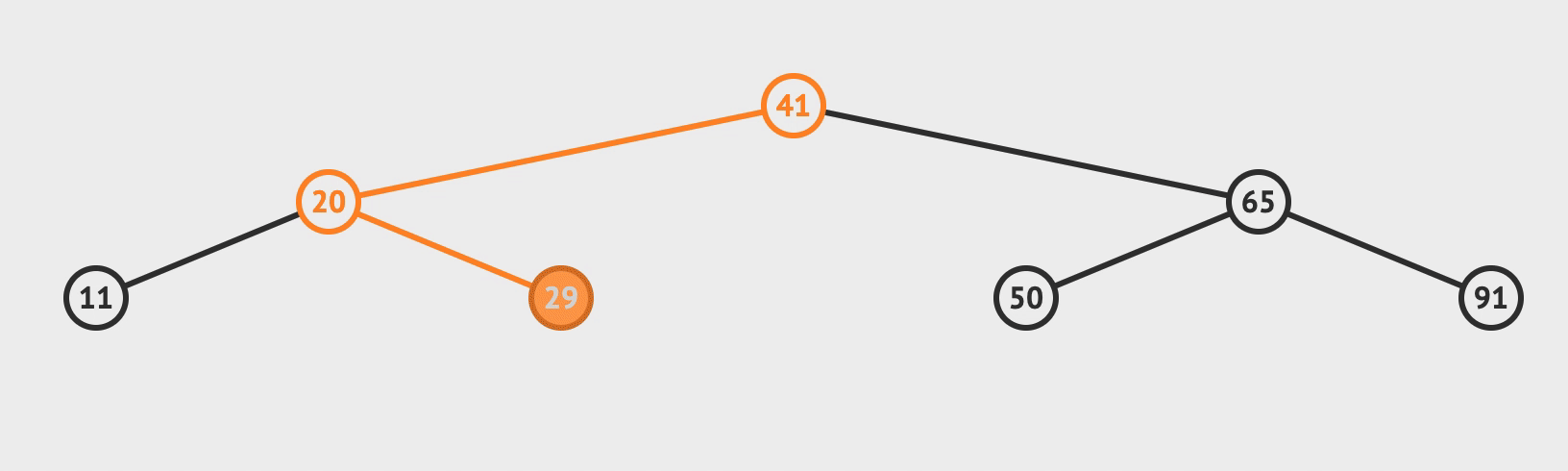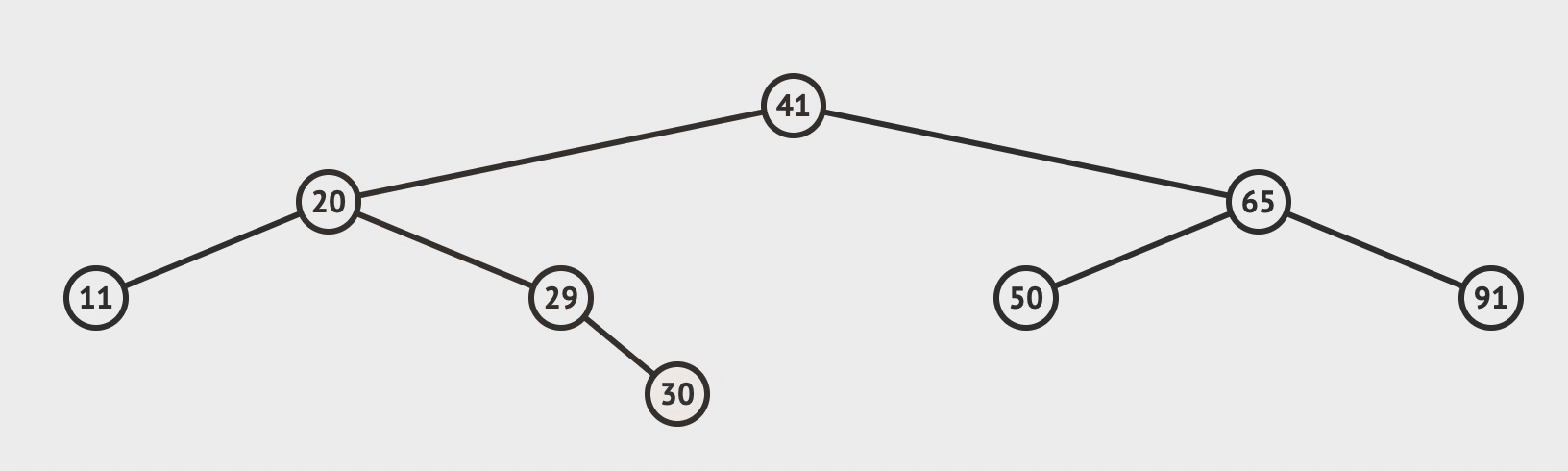
平衡:平衡因子的绝对值小于 2 (下图第一张为平衡树, 第二张为不平衡树)
- 平衡树且平衡因子==0
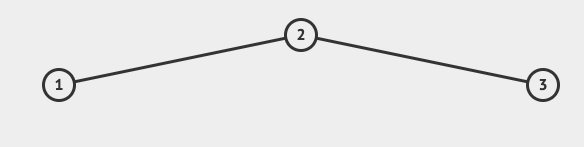
- 非平衡树且平衡因子==-2
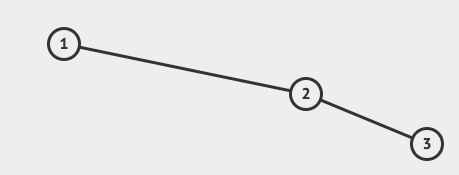
树的旋转: 参考维基百科 树的旋转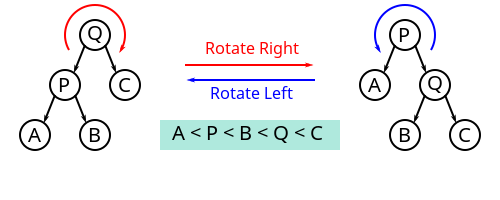
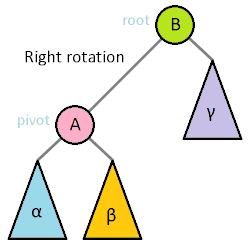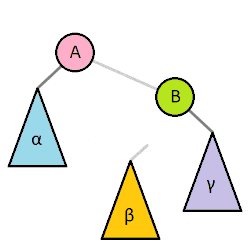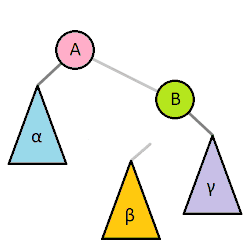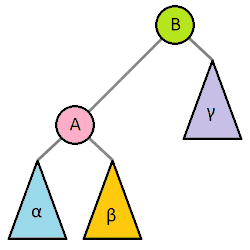
转轴的移动方向来决定它是左旋还是右旋, 本文中称转轴右移为右旋反之则是左旋
右旋: (Q为树的根节点, P为转轴, 转轴最终被右移) 右旋时,
1
2
3
转轴的右孩子 = 树的根节点;
根节点的左孩子 = 转轴的右子树根节点;
树的根节点 = 转轴;
左旋(P为树的根节点, Q为转轴, 转轴最终被左移) 左旋时,
1
2
3
转轴的左孩子 = 树的根节点;
根节点的右孩子 = 转轴的左子树根节点;
树的根节点 = 转轴;
中序不变旋转结束后二叉树的中序始终不变,A<P<B<Q<C
二、简介
AVL树(Adelson-Velsky and Landis Tree)得名于它的发明者G. M. Adelson-Velsky和Evgenii Landis,他们在1962年的论文《An algorithm for the organization of information》中公开了这一数据结构。其实AVL就是在BST的基础上增加了一个平衡(Balance)的属性, 为的是稳固算法复杂度到 O(logn), BST算法复杂度受到树结构的影响会游离于 O(logn)~O(n) 之间, 而加入了平衡属性之后则会降低到恒定为 O(logn)
三、基本特征
- 首先是 BST 的一种( BST 有的它都有)
- 是平衡二叉树(根节点的平衡因子绝对值不大于1)
- 左右子树也是平衡二叉树
四、算法描述
插入, 删除之后是否需要平衡这个树? 如何平衡?
高度
为了判断一个树是否平衡? 引入了高度这个概念, 记录从树的最后一层到当前层数的距离
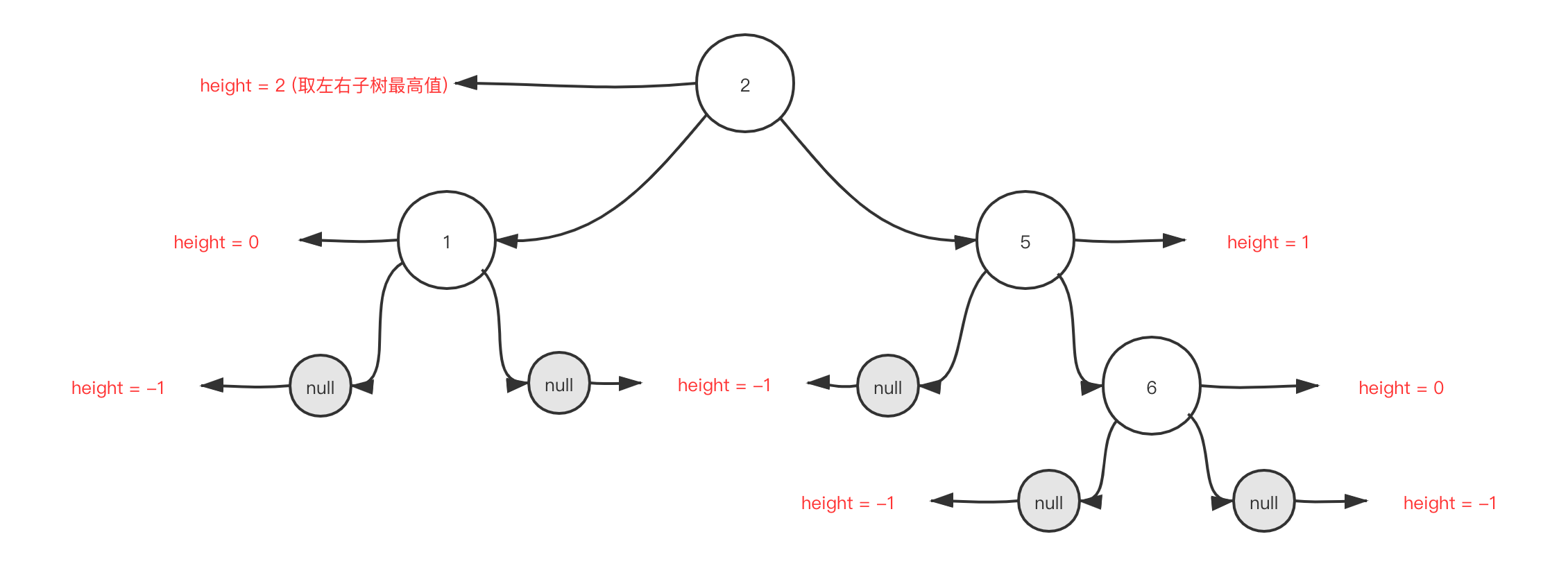
所以我们的节点(Node)结构定义如下
1
2
3
4
5
6
public static class Node {
private int data;
private int height;
private Node left;
private Node right;
}
旋转
为了解决树的平衡问题引入了树的旋转
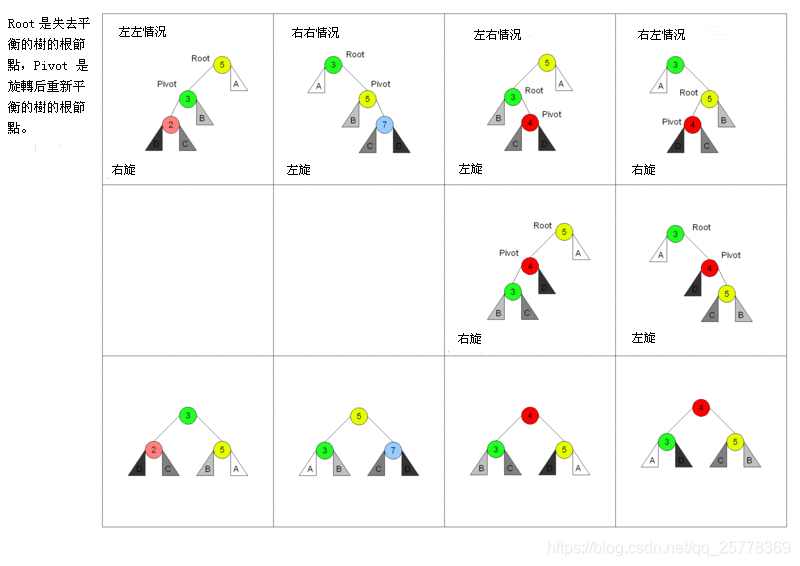
A, B, C, D代表 子节点, 子树 或者 null
左左左节点的左节点/子树导致的不平衡, 需要右旋
1
2
3
4
5
6
7
8
9
10
private Node rotateRight(Node root) {
Node t = root.left;
root.left = t.right;
t.right = root;
root.height = Math.max(height(root.left), height(root.right)) + 1;
t.height = Math.max(height(t.left), height(t.right)) + 1;
return t;
}
右右 右节点的右节点/子树导致的不平衡, 需要左旋
1
2
3
4
5
6
7
8
9
10
private Node rotateLeft(Node root) {
Node t = root.right;
root.right = t.left;
t.left = root;
root.height = Math.max(height(root.left), height(root.right)) + 1;
t.height = Math.max(height(t.left), height(t.right)) + 1;
return t;
}
左右 左节点的右节点/子树导致的不平衡, 需要左旋, 右旋
1
2
3
4
private Node rotateLeftRight(Node root) {
root.left = rotateLeft(root.left);
return rotateRight(root);
}
右左 右节点的左节点/子树导致的不平衡, 需要右旋, 左旋
1
2
3
4
private Node rotateRightLeft(Node root) {
root.right = rotateRight(root.right);
return rotateLeft(root);
}
查找
和 BST 写法一致
- 先查找根节点,
< 根, 则找左子树;> 根, 则找右子树;= 根, 则找到返回;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public Node search(int num) {
return doSearch(root, num);
}
private Node doSearch(Node root, int num) {
if (root == null) {
return null;
}
if (root.data == num) {
return root;
} else if (root.data > num) {
return doSearch(root.left, num);
} else if (root.data < num) {
return doSearch(root.right, num);
}
return null;
}
算法时间复杂度 对于 n 个节点的树
f(n) = 需要查找的次数 = 二叉树的层数 ~= O(logn)
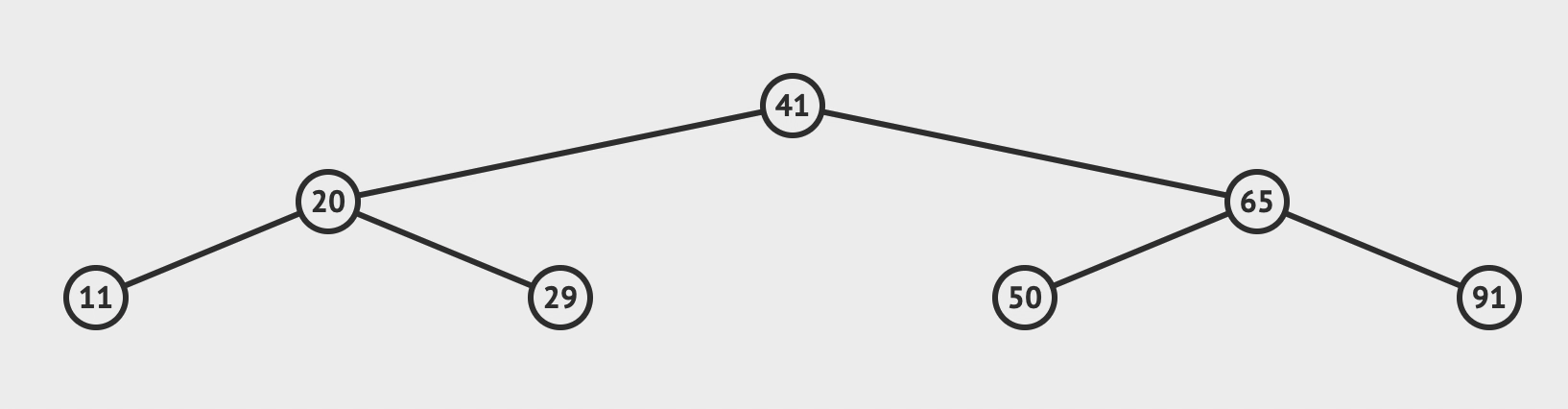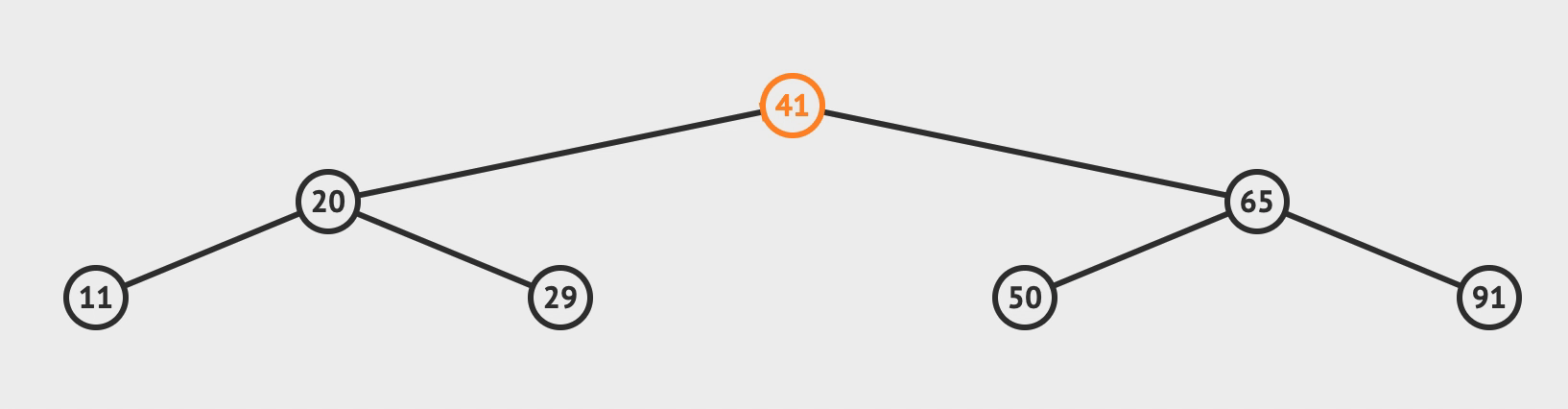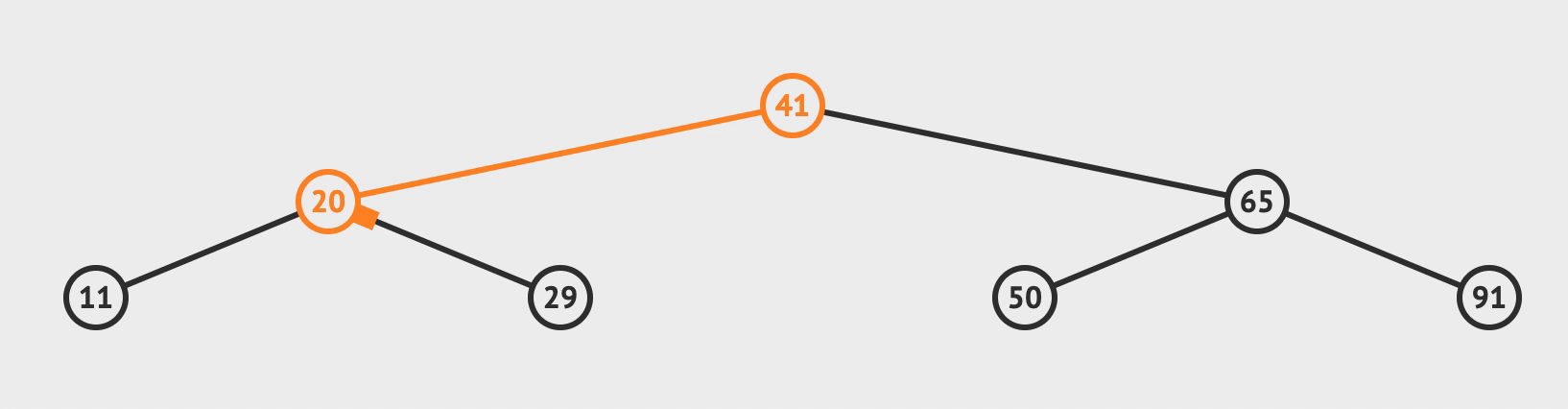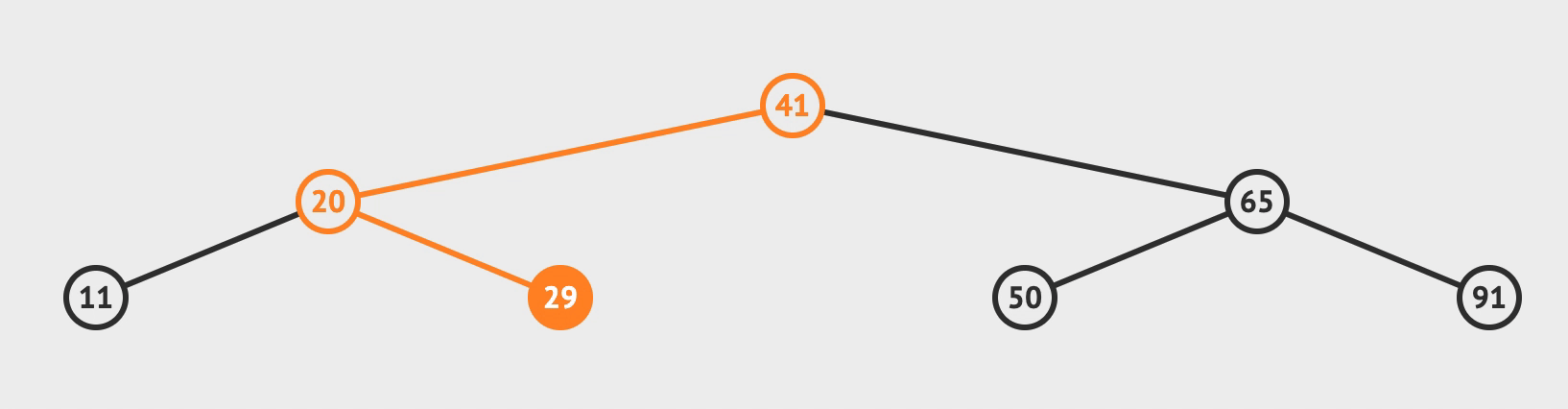
插入
- 比对根节点, 小于就往左节点比对, 大于就往右节点比对
- 直到需要比对的节点为空, 而这个空就是你需要插入的位置
- 判断树是否平衡, 否, 则需要判断旋转类型并进行旋转变换
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
public void insert(int num) {
root = doInsert(root, num);
}
private Node doInsert(Node parent, int num) {
if (parent == null) {
parent = new Node(num);
} else if (num > parent.data) {
parent.right = doInsert(parent.right, num);
// 判断树是否失衡
if (height(parent.right) - height(parent.left) >= 2) {
// '右右'
if (num > parent.right.data) {
parent = rotateLeft(parent);
}
// '右左'
else {
parent = rotateRightLeft(parent);
}
}
} else if (num < parent.data) {
parent.left = doInsert(parent.left, num);
// 判断树是否失衡
if (height(parent.left) - height(parent.right) >= 2) {
// '左左'
if (num < parent.left.data) {
parent = rotateRight(parent);
}
// '左右'
else {
parent = rotateLeftRight(parent);
}
}
}
// 重新计算旋转之后的高度
parent.height = Math.max(height(parent.left), height(parent.right)) + 1;
return parent;
}
算法时间复杂度:
f(n) = 查找插入点的比对次数logn + 一次旋转(单旋或者双旋) + 判断是否平衡 ~= O(logn)
旋转的时间复杂度 O(1) 最多需要单旋或者双旋, 另外, 判断是否平衡的时间复杂度也是 O(1) ( 主要得益于 Node 使用了 height 记录高度, 典型的空间换时间), 这样总得算法复杂度还是 比对的次数
删除
- 先查找到目标节点
- 若: 目标左子树为空, 则, 用目标右子树根节点替换目标
- 若: 目标右子树为空, 则, 用目标左子树根节点替换目标
- 若: 都不为空, 则, 选取
左子树值最大节点或者右子树最小节点替换目标, 并, 递归删除替换目标的节点 - 判断树是否平衡, 否, 则需要判断旋转类型并进行旋转变换
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
public void remove(int num) {
root = doRemove(root, num);
}
private Node doRemove(Node parent, int num) {
if (parent == null) {
return null;
}
if (num > parent.data) {
parent.right = doRemove(parent.right, num);
// 判断树是否平衡
if (height(parent.left) - height(parent.right) >= 2) {
Node t = parent.right;
// `右左`
if (t == null || height(t.right) < height(t.left)) {
parent = rotateRightLeft(parent);
}
// `右右`
else {
parent = rotateLeft(parent);
}
}
} else if (num < parent.data) {
parent.left = doRemove(parent.left, num);
// 判断树是否平衡
if (height(parent.right) - height(parent.left) >= 2) {
Node t = parent.left;
// `左右`
if (t == null || height(t.left) < height(t.right)) {
parent = rotateLeftRight(parent);
}
// `左左`
else {
parent = rotateRight(parent);
}
}
}
// 找出左子树最大的值或者右子树最小的值替换, 这里选择前者来实现
else if (parent.left != null && parent.right != null) {
// 找到左子树最大值替换
parent.data = findMax(parent.left).data;
// 删除左子树中用于替换的节点
parent.left = doRemove(parent.left, parent.data);
}
// 左子树为空, 直接用右子树根节点替换被删除的节点
else if (parent.left == null) {
parent = parent.right;
}
// 右子树为空, 直接用左子树根节点替换被删除的节点
else if (parent.right == null) {
parent = parent.left;
}
return parent;
}
private Node findMax(Node node) {
if (node == null) {
return node;
}
while (node.right != null) {
node = node.right;
}
return node;
}
算法复杂度:
f(n) = 需要比对的次数 = 查找到目标比对次数logn + 旋转次数logn = O(2logn)
最多需要 logn 次旋转, 来确保平衡, 所以最终的时间复杂度是 O(2logn)
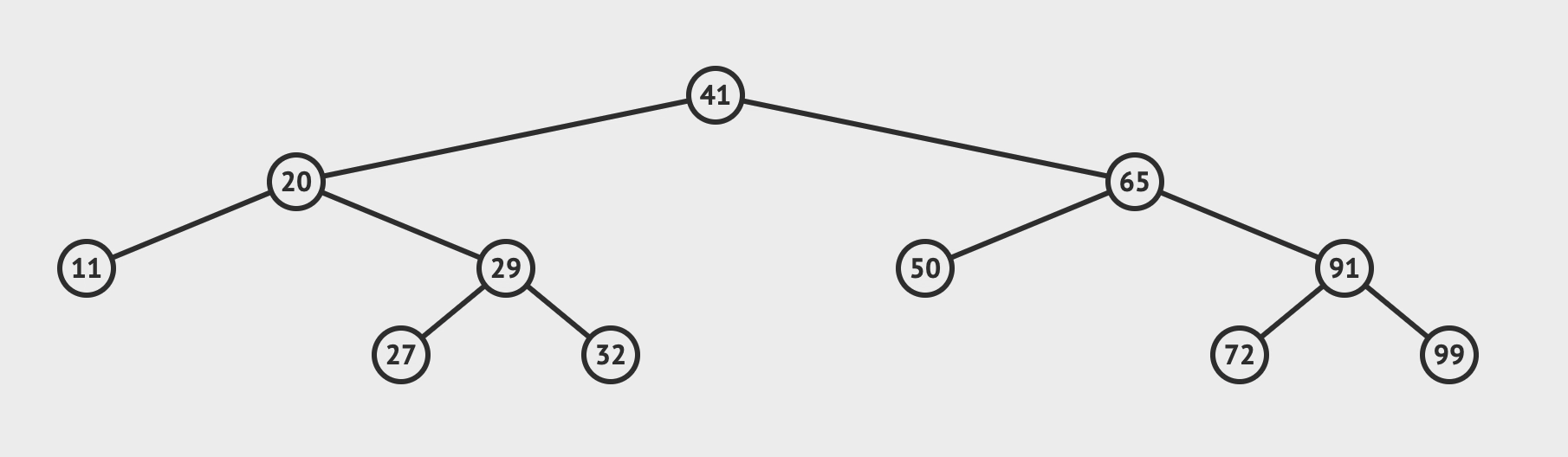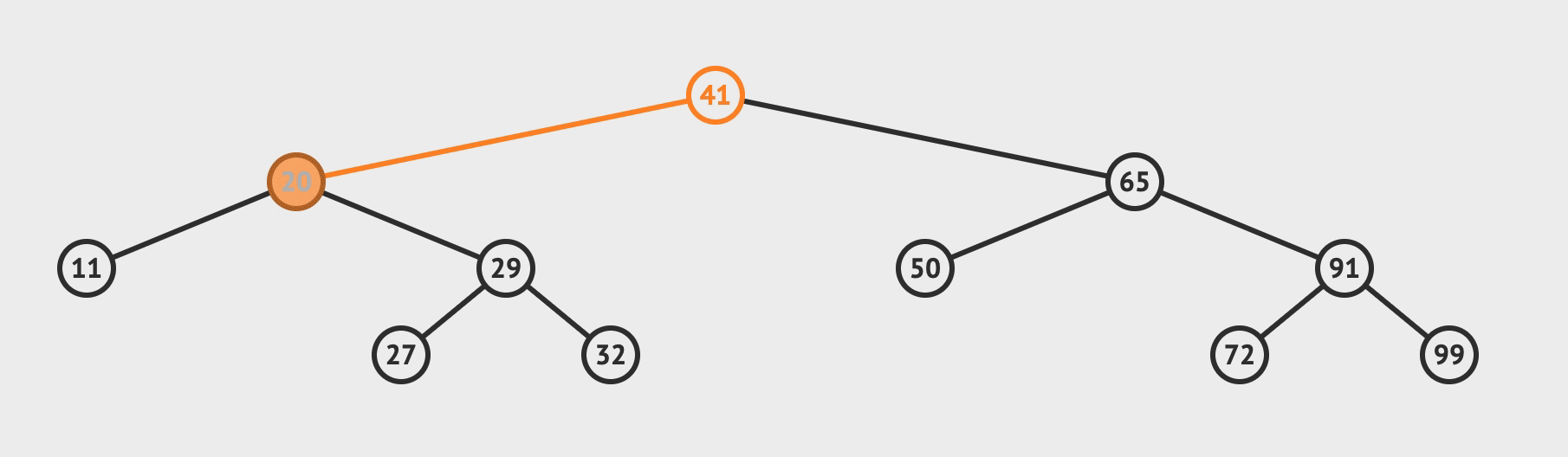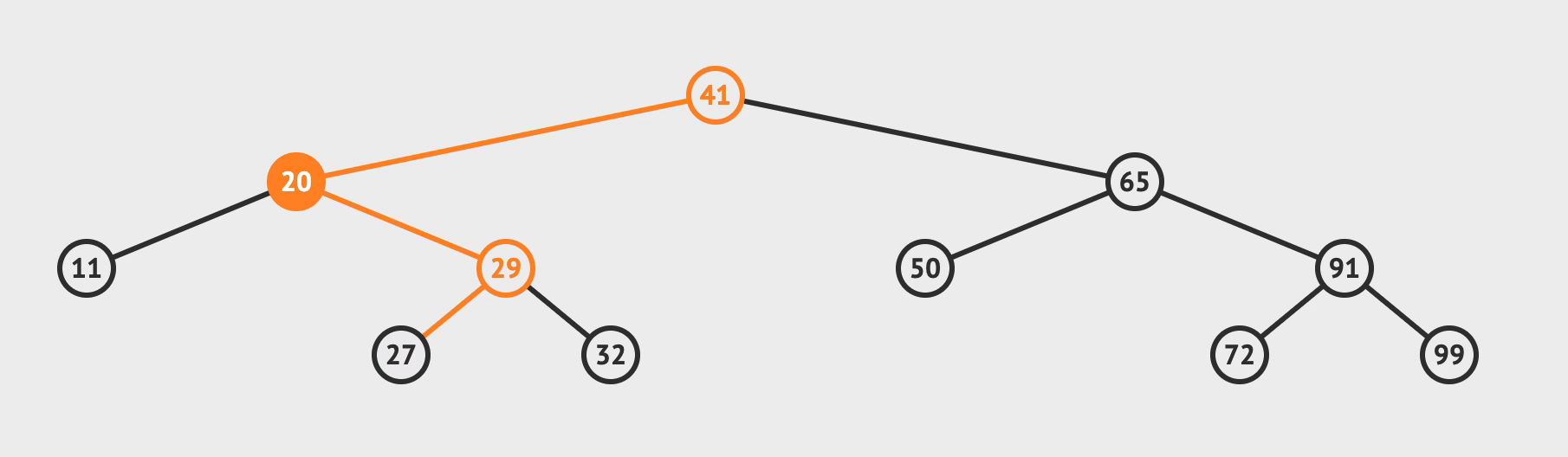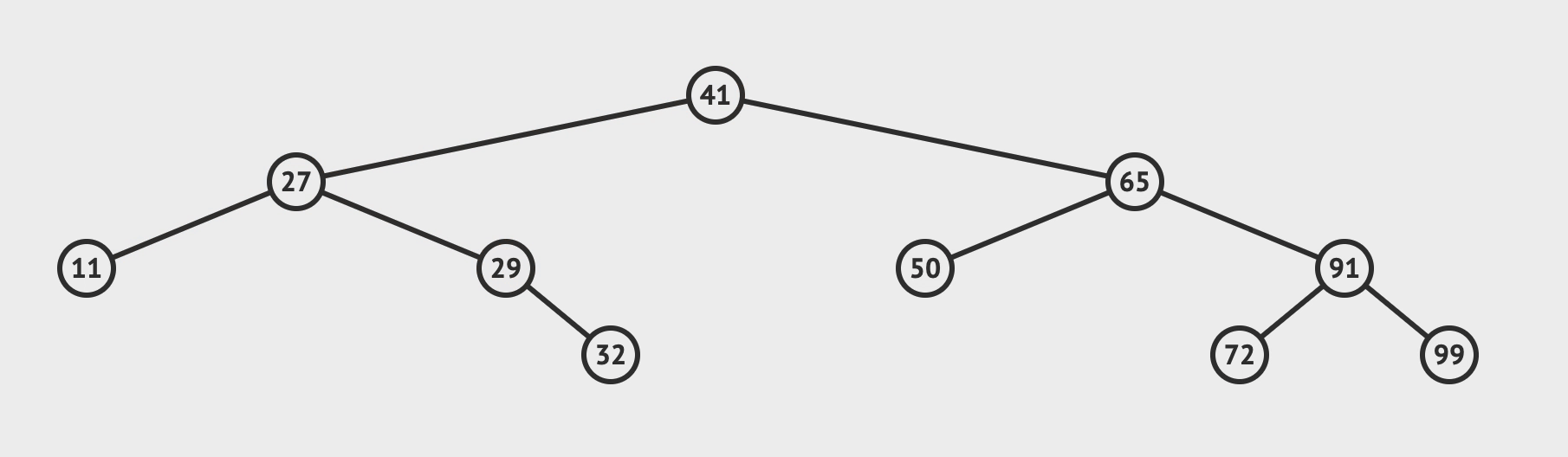
五、完整代码
就一个AVLTree.java文件搞定, 里面还附有main()函数测试功能, 可直接运行github传送门