红黑树 && BST
红黑树就是在 BST 的基础上加入了一些自己的特征
一、特征
符合 BST 所有特征- 节点有两色, 红, 黑
- 根是黑
- 所有叶子节点是黑 (叶子是NIL节点)
- 每个红色节点必须有两个黑节点
- 任意节点到每个叶子节点的路径都包含相同数量的黑节点

这些特征保证了, 根到叶子节点的最长路径, 最长不会超过最短路径的 2 倍 因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例,这个在高度上的理论上限允许红黑树在最坏情况下都是高效的, 而不同于 BST
如何理解 路径max <= 路径min * 2, 看看性质 4, 导致路径中不会有两个相连的红节点, 最短的可能路径是全黑路径, 最长的可能路径是红黑交替路径, 又性质 5, 每个路径黑色节点数一致, 得出, 最长和最短拥有相同数量的黑节点, 表明不可能超过两倍
所有节点一定有两个黑色的空叶子节点(NIL节点), 很多文章没画出来也是默认有的
二、算法描述
0. 节点结构
1
2
3
4
5
public static class Node {
public Node left, right, parent;
public boolean black = false;
public int value;
}
1. 查找
- 先查找根节点,
< 根, 则找左子树;> 根, 则找右子树;= 根, 则找到返回;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public Node search(int num) {
return doSearch(root, num);
}
private Node doSearch(Node root, int num) {
if (root == null) {
return null;
}
if (root.value == num) {
return root;
} else if (root.value > num) {
return doSearch(root.left, num);
} else if (root.value < num) {
return doSearch(root.right, num);
}
return null;
}
算法时间复杂度 对于 n 个节点的树
最优f(n) = 需要查找的次数 = 二叉树的层数 ~= O(logn)
最差f(n) = 需要查找的次数 = 二叉树的层数 = n = O(n)
但是由于我们插入算法的原因, 基本维持在O(logn)左右
2. 插入
首先需要明白的前提是:
- 所有的插入操作都是在叶子节点进行的;
- 我们默认插入节点都是红色, 这样就不会增加树的高度了, 因为如果树的高度增加, 势必会迭代到父节点里面去处理红黑树黑节点高度平衡问题
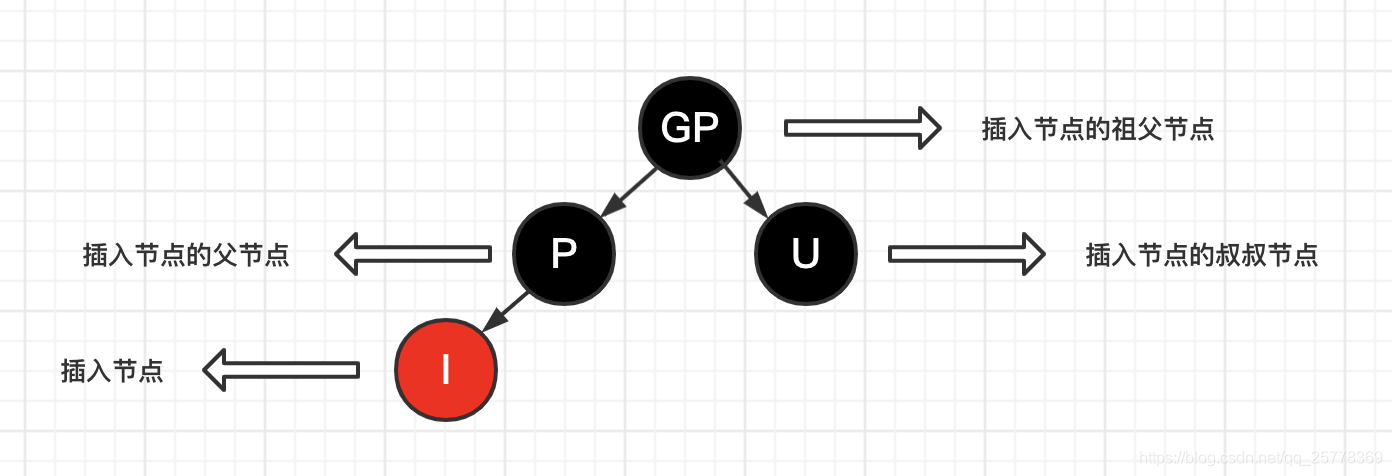
- 以下图示约定:
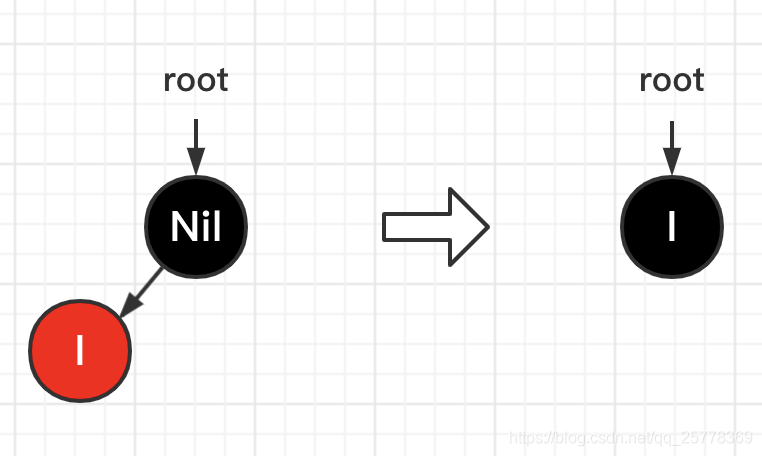
case 1: 插入的是空树
操作:
- I 颜色置黑
- I 赋值给
root
case 2: 插入节点值重复
操作:
- 直接返回, 无操作
case 3: 父节点是黑
操作:
- 无操作, 不需要修复平衡
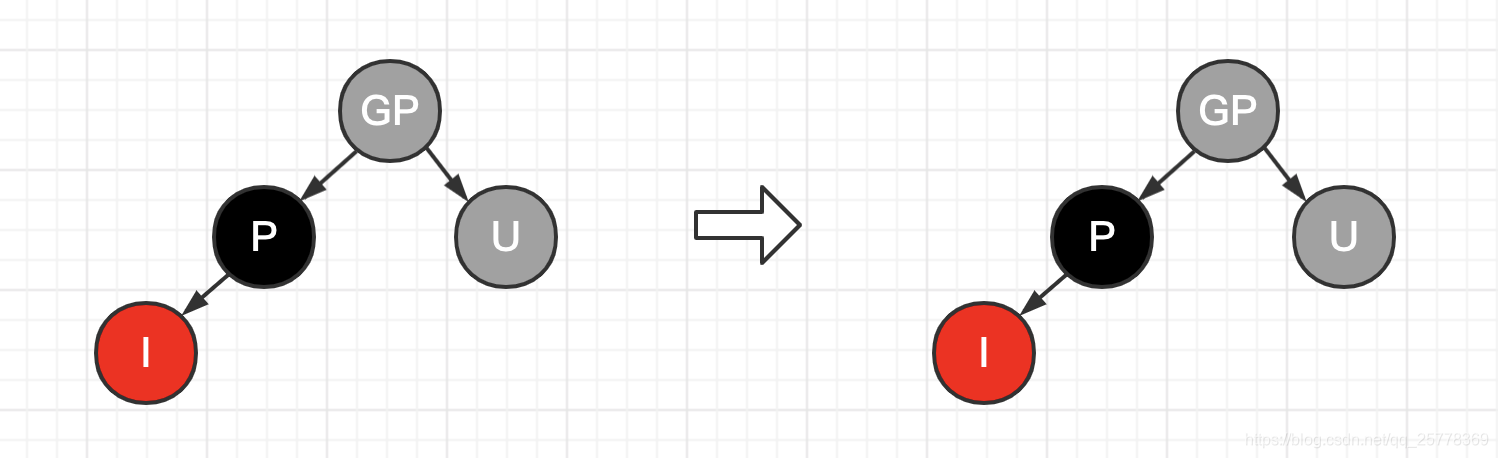
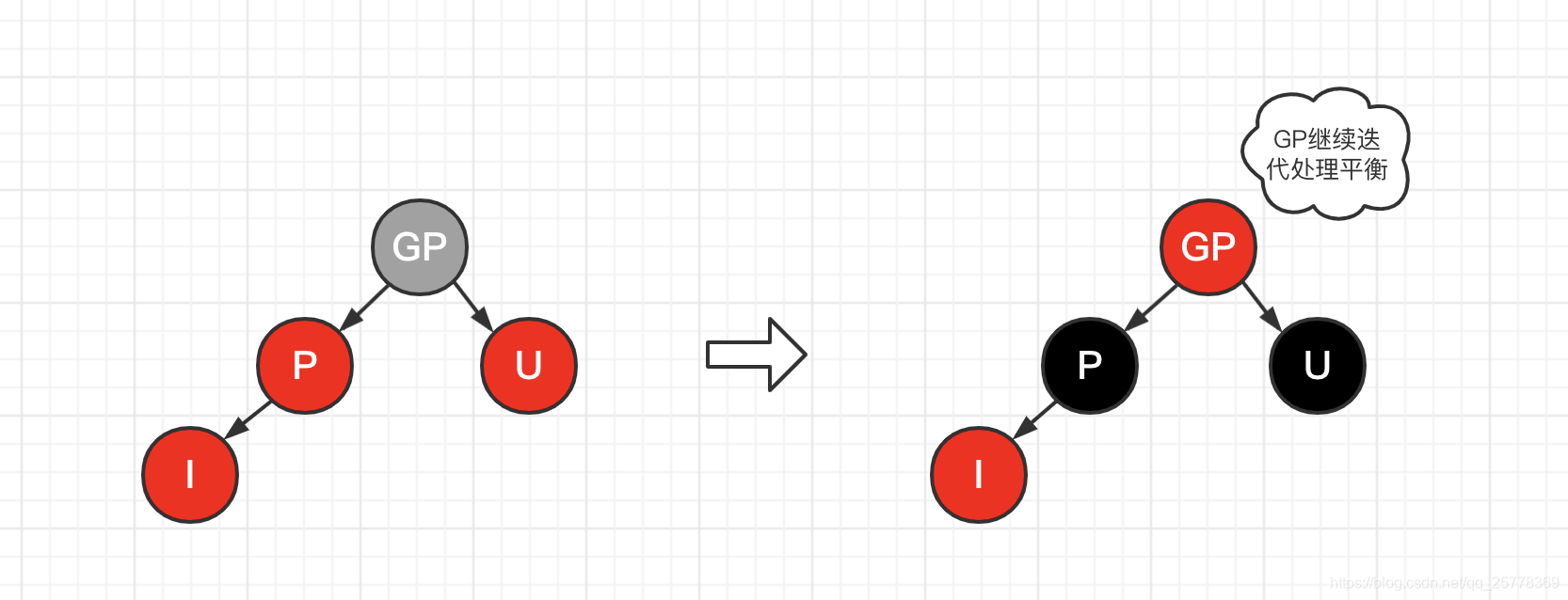
case 4: 父节点是红, 叔节点是红
操作:
- P 和 U 置黑
- GP 置红
- GP 作为插入点, 继续迭代一遍, 平衡红黑树
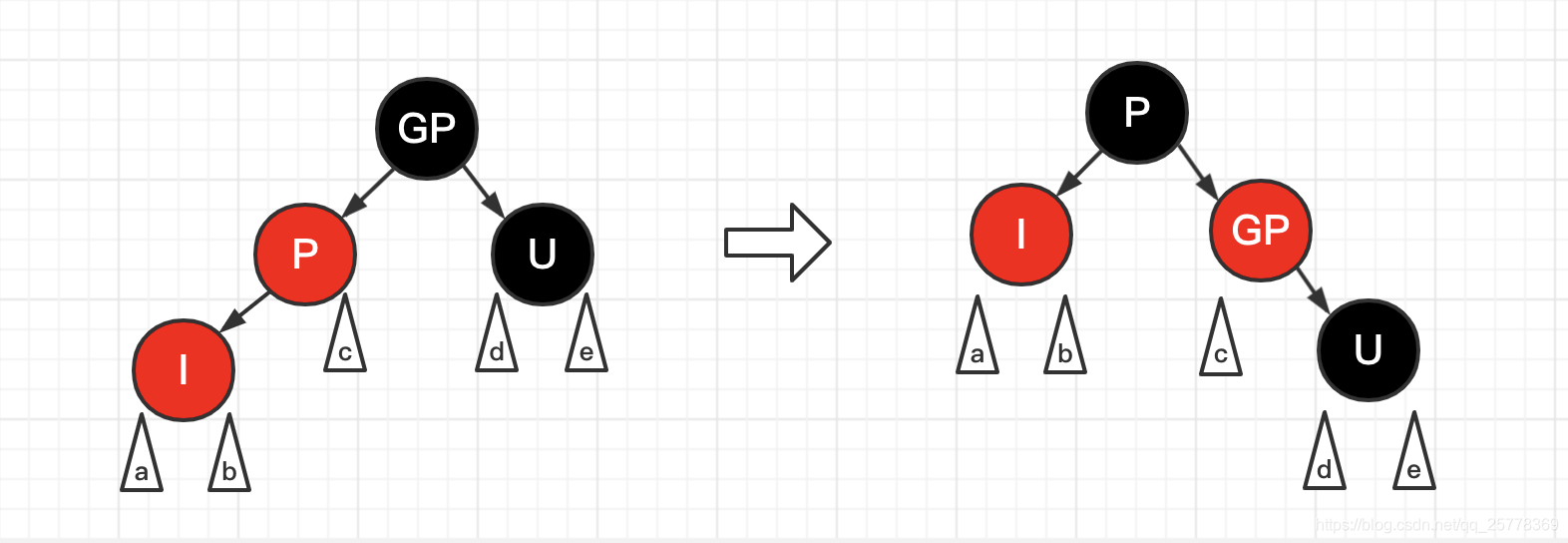
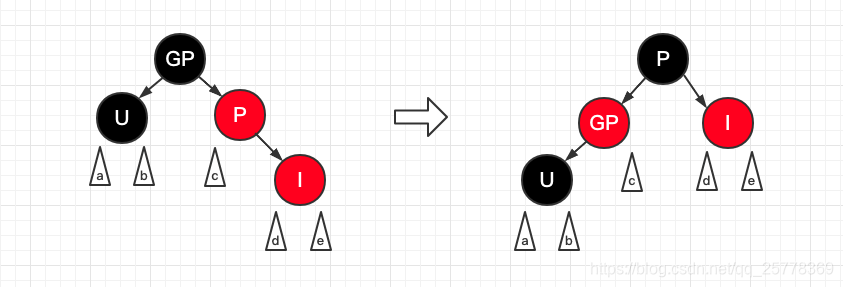
case 5: 父节点是红, 叔节点是黑/Nil, 左左
操作:
- GP 置红
- P 置黑
- GP 右旋
左左: P是GP的左儿子, I是P的左儿子右旋之后: 树的每条路径黑节点数量并没有增加, 符合特征6, 至此树平衡结束三角形: 代表子树, 可能由 case 4, case 7, case 8,递归到本case 导致有子树结构
case 6: 父节点是红, 叔节点是黑/Nil, 右右
操作:
- GP 置红
- P 置黑
- GP 左旋
右右: P是GP的右儿子, I是P的右儿子右旋之后: 树的每条路径黑节点数量并没有增加, 符合特征6, 至此树平衡结束三角形: 代表子树, 可能由 case 4, case 7, case 8,递归到本case 导致有子树结构
case 7: 父节点是红, 叔节点是黑/Nil, 左右
操作:
- GP 置红
- P 置黑
- P 左旋
- 继续执行 case 5 逻辑
左右: P是GP的左儿子, I是P的右儿子左旋之后: 转变成了 case 5三角形: 代表子树, 可能由 case 4 递归到本case 导致有子树结构
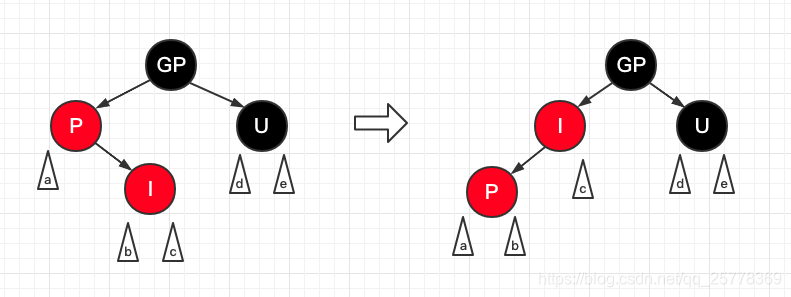
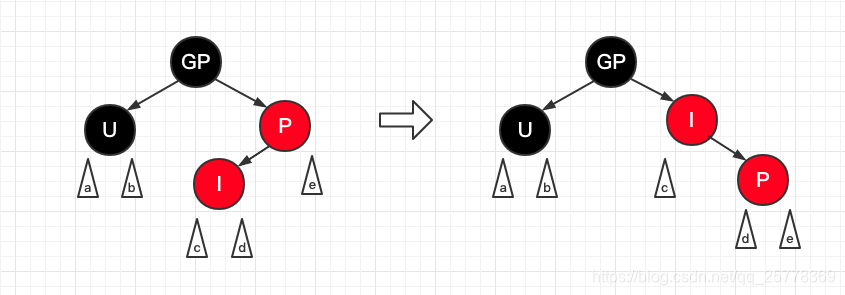
case 8: 父节点是红, 叔节点是黑/Nil, 右左
操作:
- GP 置红
- P 置黑
- P 右旋
- 继续执行 case 6 逻辑
右左: P是GP的右儿子, I是P的左儿子右旋之后: 转变成了 case 6三角形: 代表子树, 可能由 case 4 递归到本case 导致有子树结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
public void insert(int v) {
final Node node = new Node();
node.left = node.right = node.parent = null;
node.black = false;
node.value = v;
// case 1: 插入节点是根
if (root == null) {
root = node;
root.black = true;
return;
} else {
Node p = findParent(v);
// case 2: 插入值重复
if (p == null) {
return;
}
setParent(node, p);
if (v > p.value) {
p.right = node;
} else {
p.left = node;
}
fixInsert(node);
}
}
// 找到属于v的parent准备插入
private Node findParent(int v) {
Node pre = root;
Node index = root;
while (index != null) {
// 找到相同值直接返回
if (index.value == v) {
return null;
}
pre = index;
index = v < index.value ? index.left : index.right;
}
return pre;
}
// 平衡红黑树
private void fixInsert(Node node) {
final Node parent = node.parent;
final Node uncle = node.uncle();
final Node grandparent = node.grandparent();
// case 1: 插入节点是根
if (parent == null) {
root = node;
root.black = true;
}
// case 3: 插入节点的 父亲 是黑
else if (parent != null && parent.black) {
// do nothing
}
else if (parent != null && !parent.black) {
// case 4: 插入节点的 父亲 是红, 叔叔 也是红
if (uncle != null && !uncle.black) {
parent.black = true;
uncle.black = true;
// 有叔叔必定有祖父
grandparent.black = false;
// 祖父的父亲是 红, 和祖父冲突了
fixInsert(grandparent);
}
else if (uncle == null || uncle.black) {
// case 5: 叔叔 是黑/空, `左左`
if (parent == grandparent.left && node == parent.left) {
parent.black = true;
grandparent.black = false;
rotateRight(grandparent);
}
// case 6: 叔叔 是黑/空, `左右`
else if (parent == grandparent.left && node == parent.right) {
rotateLeft(parent);
fixInsert(parent);
}
// case 7: 叔叔 是黑/空, `右右`
else if (parent == grandparent.right && node == parent.right) {
parent.black = true;
grandparent.black = false;
rotateLeft(grandparent);
}
// case 8: 叔叔 是黑/空, `右左`
else if (parent == grandparent.right && node == parent.left) {
rotateRight(parent);
fixInsert(parent);
}
}
}
}
算法时间复杂度
对于有n个节点的树(由于树的高度趋近logn), f(n) = logn次左右查找对比 + 最多只需要2次旋转 + logn次的颜色替换 = O(logn) + O(1) + O(1) = O(logn)
由于颜色替换十分迅速, 这里可以把logn次替换看成是O(1)复杂度
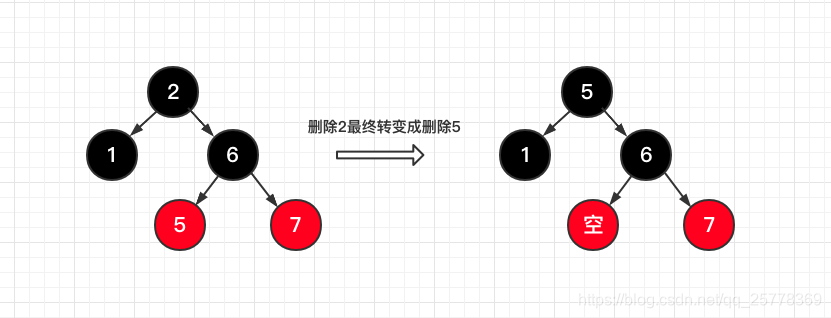
3. 删除
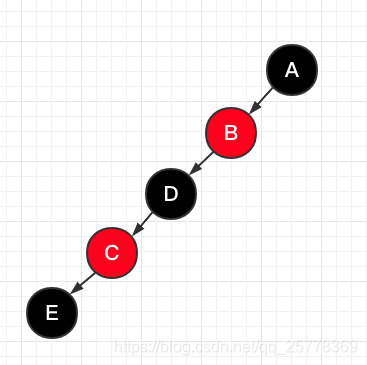
需要明白的是, 所有的删除操作最终都会变成删除一个叶子节点, 比如下图
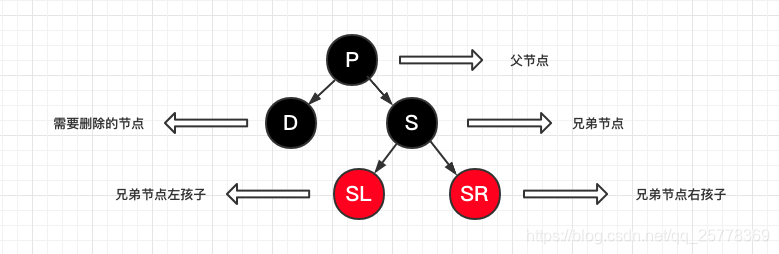
以下图示约定
case 1: 树空
操作:
- 删除失败
case 2: 无匹配项
操作:
- 删除失败
case 3: d 是红
操作:
- 直接删除
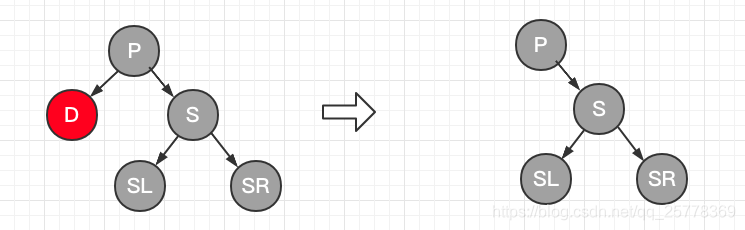
case 4: d 是黑, s 是红
操作:
- P 置红
- S 置黑
- P 左旋(D 是左儿子) 或者 右旋(D 是右儿子)
- 旋转之后兄弟节点就变为黑色了, 递归到下面的 case 5, 6, 7 进行处理
三角形: 代表子树, 可能由 case 7,递归到本case 导致有子树结构递归处理: 之所以需要递归处理, 是因为在旋转之后, 所有路径的黑色节点数和旋转前一样, 若 D节点路径中少了一个黑色节点, 不满足性质6了,需要递归处理一下
P 左旋(D 是左儿子)
右旋(D 是右儿子)
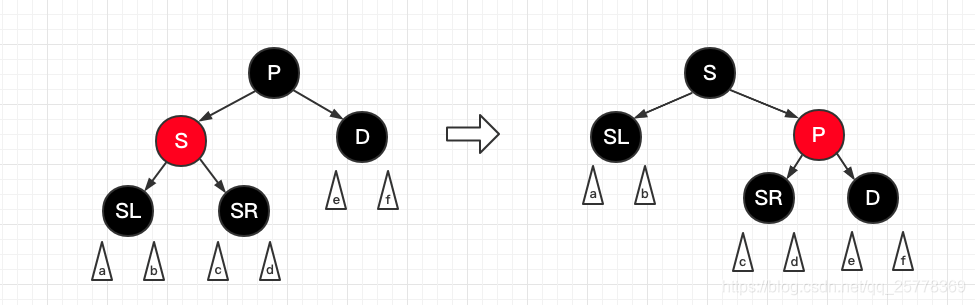
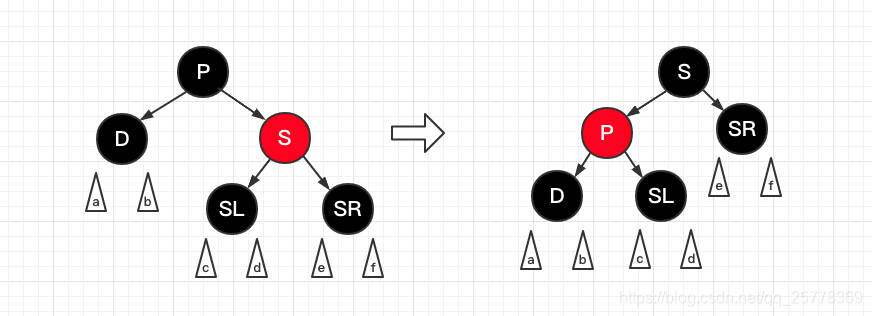
case 5.1: d 是黑, s 是黑, s 右孩子是红 且 d 是左孩子
操作:
- P 和 S 颜色互换
- P 左旋
三角形: 代表子树, 可能由 case 4,6,7 ,递归到本case 导致有子树结构左旋: 左旋之后直接平衡了, 可以由下图, 看出, 所有路径旋转之后 D 节点路径中多了一个黑色节点, 其他路径黑色节点数都没变化, 而我们恰巧需要删除 D节点中的一个黑色节点, 至此, 满足性质6, 红黑树刚好平衡
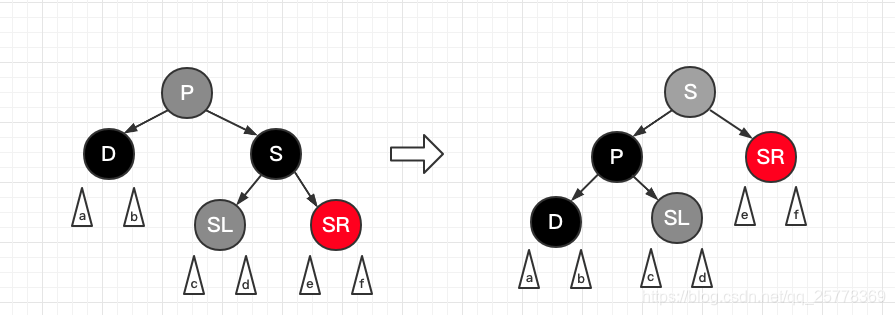
case 5.2: d 是黑, s 是黑, s 左孩子是红 且 d 是右孩子
操作:
- P 和 S 颜色互换
- P 右旋
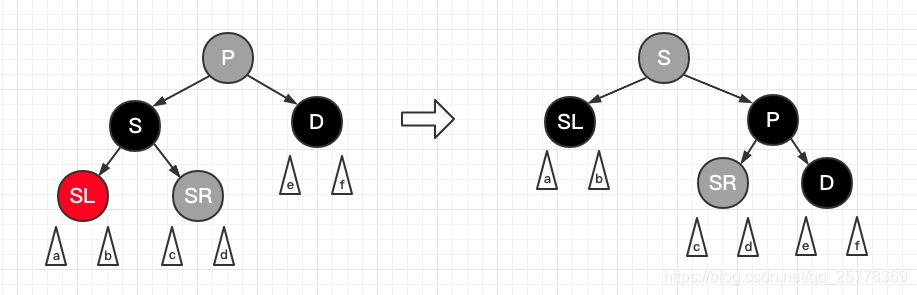
case 6.1: d 是黑, s 是黑, s 左孩子是红 且 d 是左孩子
操作:
- S 置红, SL 置黑
- S 右旋
- 树的结构就切换成了 case 5.1 的模样, 递归使用 case 5.1 解决
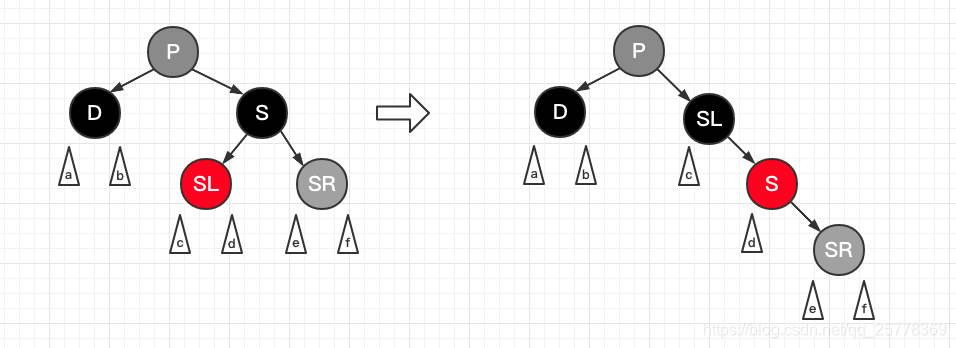
case 6.2: d 是黑, s 是黑, s 右孩子是红 且 d 是右孩子
操作:
- S 置红, SR 置黑
- S 左旋
- 树的结构就切换成了 case 5.2 的模样, 递归使用 case 5.2 解决
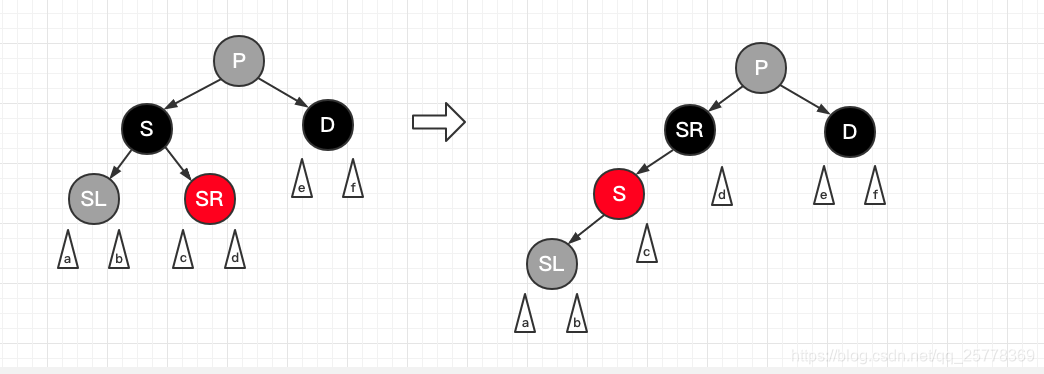
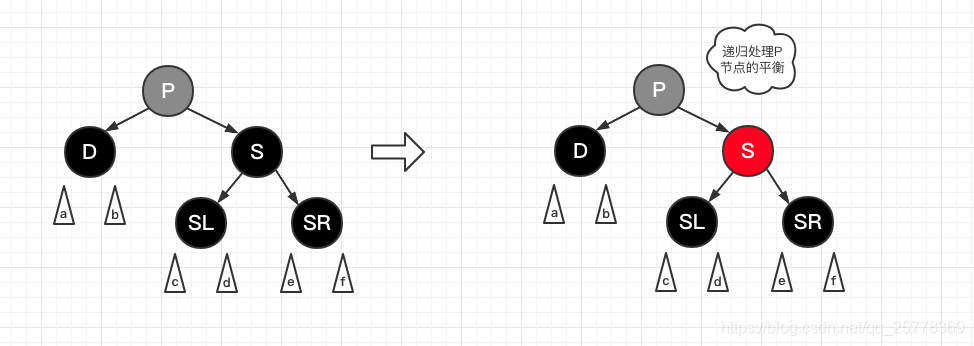
case 7: d 是黑, s sl sr 全是黑
操作:
- S 置红
- 递归 P 节点, 平衡红黑树
递归: S 置红会导致右子树路径上黑节点数量少1, 左子树由于 D(黑节点) 将被删除, 所以路径上黑节点数也会少1, 符合性质6, 但是此时 P 所在树整体所有路径黑色节点数少1, 需要向上递归平衡红黑树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
public Node remove(int num) {
// case 1: 树空, 删除失败
if (root == null) {
return null;
} else {
final Node numNode = findNum(root, num);
// case 2: 无匹配项, 删除失败
if (numNode == null) {
return null;
}
// 此时, replaceNode 一定是个叶子节点
final Node replaceNode = findReplaceNode(numNode);
if (replaceNode.black) {
// 所有的删除操作最后都被转换成一种情况, 删除一个叶子节点
fixRemove(replaceNode);
}
replaceNode.value = num;
replaceNode.black = numNode.black;
if (replaceNode.parent != null) {
if (replaceNode.parent.left == replaceNode) {
replaceNode.parent.left = null;
} else {
replaceNode.parent.right = null;
}
}
replaceNode.parent = null;
return replaceNode;
}
}
// 平衡红黑树
// r: 替换的节点
private void fixRemove(Node d) {
final Node p = d.parent;
final Node s = d.sibling();
final Node sL = d.siblingLeft();
final Node sR = d.siblingRight();
// case 1: 替换的是根节点
if (root == d) {
root = null;
}
// case 3: 替换的是 红
else if (!d.black) {
// do nothing
d.black = true;
}
// 替换的是 黑
else if (d.black) {
// case 4: s 是红, 可以借, 旋转
if (s != null && !s.black) {
p.black = false;
s.black = true;
if (s == p.left) {
rotateRight(p);
} else {
rotateLeft(p);
}
fixRemove(d);
} else if ((s == null || s.black)) {
// case 5.1: s是黑, sL是红, r是p的右节点
if ((sL != null && !sL.black) && d == p.right) {
s.black = p.black;
p.black = true;
sL.black = true;
rotateRight(p);
}
// case 5.2: s是黑, sR是红, r是p的左节点
else if ((sR != null && !sR.black) && d == p.left) {
s.black = p.black;
p.black = true;
sR.black = true;
rotateLeft(p);
}
// case 6.1: s是黑, sL是红, r是p的左节点
else if ((sL != null && !sL.black) && d == p.left) {
s.black = false;
sL.black = true;
rotateRight(s);
fixRemove(d);
}
// case 6.2: s是黑, sR是红, r是p的右节点
else if ((sR != null && !sR.black) && d == p.right) {
s.black = false;
sR.black = true;
rotateLeft(s);
fixRemove(d);
}
}
// case 7: s == sL == sR 全黑
else if ((s == null || s.black) && (sL == null || sL.black) && (sR == null || sR.black)) {
s.black = false;
fixRemove(p);
}
}
}
算法时间复杂度
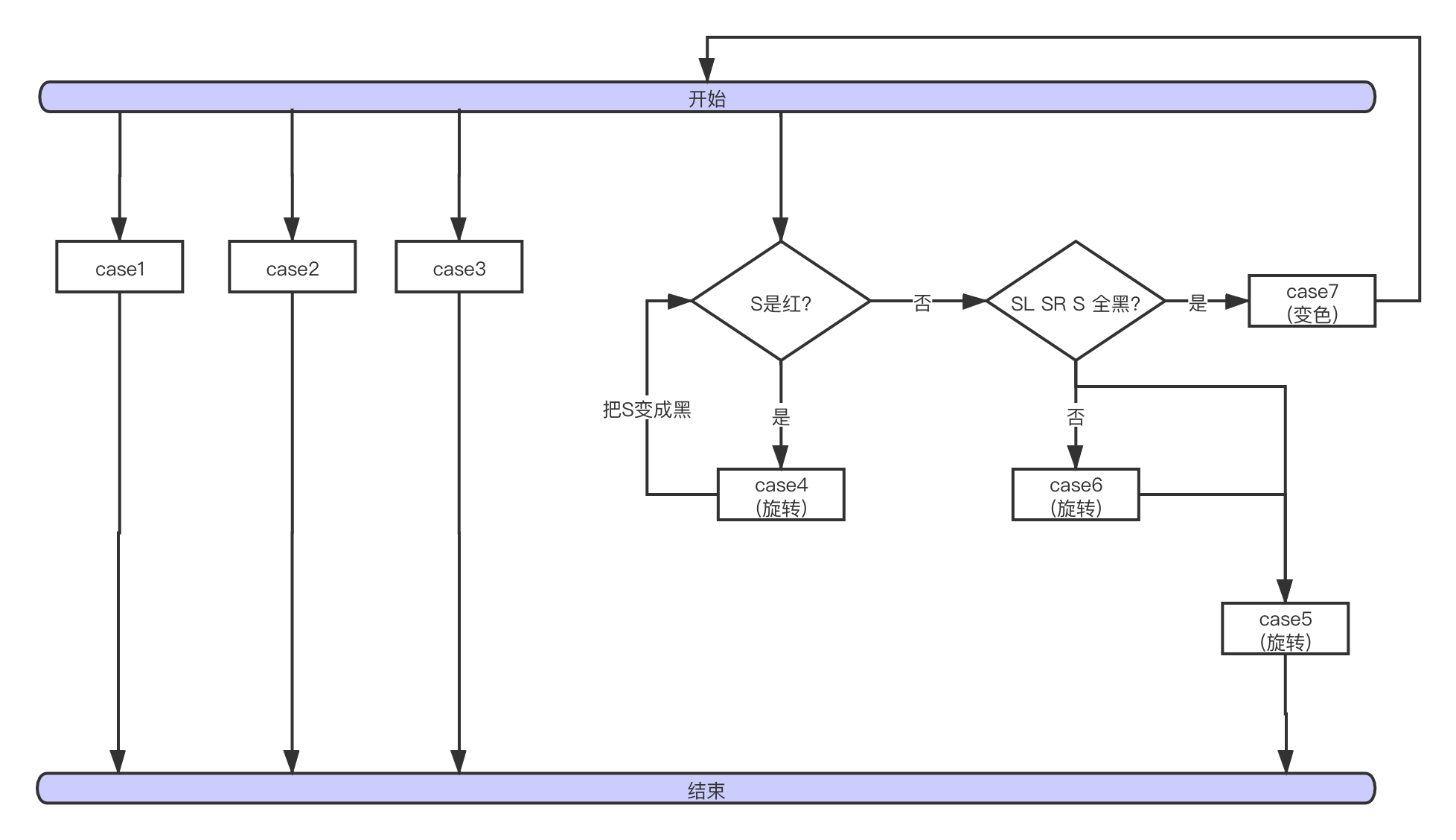
从流程图看:
对于有n个节点的树(由于树的高度趋近logn), f(n) = 查找替换比对次数logn + 变色次数logn + case4 旋转次数logn + case5,6旋转次数2 = 2logn
变色次数logn: 由于变色操作消耗较小, 故可以看成是 O(1)
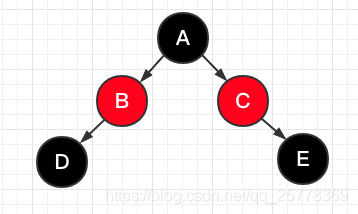
不对啊, 网上不都说至多旋转三次吗? 怎么从流程图看 case4旋转 会被调用logn次???
别急, 这里先上结论, 一旦经过 case 4 后就不可能再有 case 7 了, 所以删除至多只有三次旋转, 最终的算法时间复杂度 logn
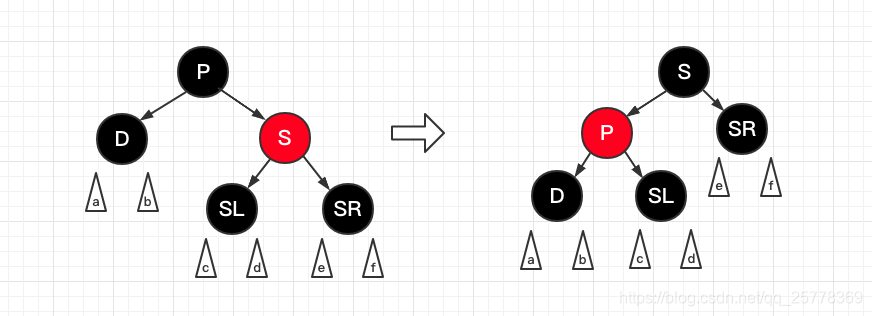
上图是截取的 case 4 场景, 分析一下, 旋转之后 D 一定黑, S 一定黑, P一定红, 此时, 我们进入case 7 瞧瞧
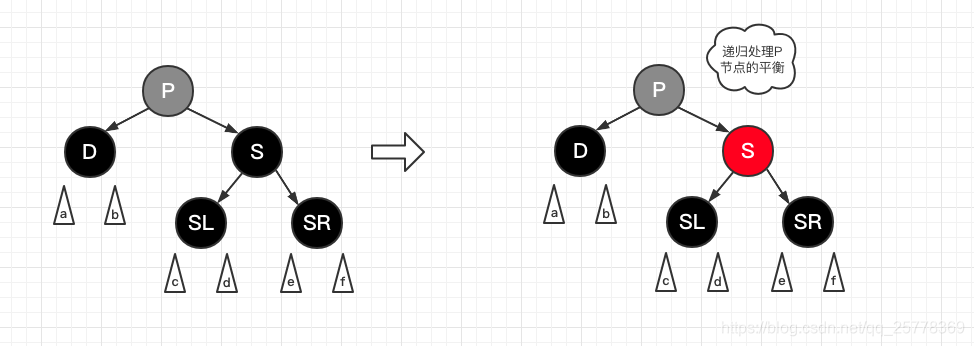
可得: 上图 P一定红, 在 S 变红之后, 只需要将 P直接转黑就行, 树就平衡了
三、完整代码
就一个RBTree.java文件搞定, 里面还附有main()函数测试功能, 可直接运行github传送门